Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T09:31:08.291Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A LATTICE GENERALISATION OF THE LOGARITHM AND A DEFORMATION OF THE DEDEKIND ETA FUNCTION

Part of: Other special functions Optimality conditions Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  20 February 2020

LAURENT BÉTERMIN Open the ORCID record for LAURENT BÉTERMIN [Opens in a new window]
LAURENT BÉTERMIN*
Affiliation:
Faculty of Mathematics, University of Vienna, Oskar-Morgenstern-Platz 1, 1090 Vienna, Austria email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a deformation 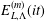$E_{L,\unicode[STIX]{x1D6EC}}^{(m)}(it)$ of the Dedekind eta function depending on two 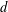$d$-dimensional simple lattices 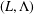$(L,\unicode[STIX]{x1D6EC})$ and two parameters 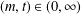$(m,t)\in (0,\infty )$, initially proposed by Terry Gannon. We show that the minimisers of the lattice theta function are the maximisers of 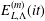$E_{L,\unicode[STIX]{x1D6EC}}^{(m)}(it)$ in the space of lattices with fixed density. The proof is based on the study of a lattice generalisation of the logarithm, called the lattice logarithm, also defined by Terry Gannon. We also prove that the natural logarithm is characterised by a variational problem over a class of one-dimensional lattice logarithms.

Keywords

Dedekind eta functiontheta functionlatticeoptimisation

MSC classification

Primary: 33E20: Other functions defined by series and integrals
Secondary: 11F20: Dedekind eta function, Dedekind sums 49K30: Optimal solutions belonging to restricted classes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 1 , August 2020 , pp. 118 - 125
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Cambridge University Press 2020

Footnotes

This research is supported by Villum Fonden via the QMATH Centre of Excellence (Grant No. 10059).

References

Bergman, O., Gaberdiel, M. R. and Green, M. B., ‘D-brane interactions in type IIB plane-wave background’, J. High Energy Phys. 2003 (2003), 002.10.1088/1126-6708/2003/03/002CrossRefGoogle Scholar
Bétermin, L., ‘Two-dimensional theta functions and crystallization among Bravais lattices’, SIAM J. Math. Anal. 48(5) (2016), 3236–3269.10.1137/15M101614XCrossRefGoogle Scholar
Bétermin, L., ‘Minimizing lattice structures for Morse potential energy in two and three dimensions’, J. Math. Phys. 60(10) (2019), 102901.10.1063/1.5091568CrossRefGoogle Scholar
Bétermin, L. and Knüpfer, H., ‘On Born’s conjecture about optimal distribution of charges for an infinite ionic crystal’, J. Nonlinear Sci. 28(5) (2018), 1629–1656.10.1007/s00332-018-9460-3CrossRefGoogle Scholar
Bétermin, L. and Knüpfer, H., ‘Optimal lattice configurations for interacting spatially extended particles’, Lett. Math. Phys. 108(10) (2018), 2213–2228.10.1007/s11005-018-1077-9CrossRefGoogle Scholar
Brauchart, J. S. and Grabner, P., ‘Distributing many points on spheres: minimal energy and designs’, J. Complexity 31 (2015), 293–326.10.1016/j.jco.2015.02.003CrossRefGoogle Scholar
Cohn, H. and Kumar, A., ‘Universally optimal distribution of points on spheres’, J. Amer. Math. Soc. 20(1) (2007), 99–148.10.1090/S0894-0347-06-00546-7CrossRefGoogle Scholar
Cohn, H., Kumar, A., Miller, S. D., Radchenko, D. and Viazovska, M., ‘Universal optimality of the E8 and Leech lattices and interpolation formulas’, Preprint, 2019, arXiv:1902:05438.Google Scholar
Epstein, P., ‘Zur Theorie allgemeiner Zetafunctionen’, Math. Ann. 56(4) (1903), 615–644.CrossRefGoogle Scholar
Faulhuber, M., ‘Extremal determinants of Laplace–Beltrami operators for rectangular tori’, Preprint, 2017, arXiv:1709.06006.Google Scholar
Gannon, T., ‘Variations on Dedekind’s eta’, in: Symmetry in Physics: in Memory of Robert T. Sharp, CRM Proceedings and Lecture Notes, 34 (American Mathematical Society, Providence, RI, 2005), 55–66.Google Scholar
Krazer, A. and Prym, E., Neue Grundlagen einer Theorie der allgemeinen Theta-funktionen (Teubner, Leipzig, 1893).Google Scholar
Luo, S., Ren, X. and Wei, J., ‘Non-hexagonal lattices from a two species interacting system’, Preprint, 2019, arXiv:1902.09611.Google Scholar
Miller, K. S. and Samko, S. G., ‘Completely monotonic functions’, Integral Transforms Spec. Funct. 12 (2001), 389–402.10.1080/10652460108819360CrossRefGoogle Scholar
Montgomery, H. L., ‘Minimal theta functions’, Glasg. Math. J. 30(1) (1988), 75–85.10.1017/S0017089500007047CrossRefGoogle Scholar
Nikiforov, A. F. and Uvarov, V. B., Special Functions in Mathematical Physics. A Unified Introduction with Applications (Birkhäuser, Basel, 1988).Google Scholar
Osgood, B., Phillips, R. and Sarnak, P., ‘Extremals of determinants of Laplacians’, J. Funct. Anal. 80 (1988), 148–211.10.1016/0022-1236(88)90070-5CrossRefGoogle Scholar
Rankin, R. A., ‘A minimum problem for the Epstein zeta-function’, Proc. Glasg. Math. Assoc. 1(4) (1953), 149–158.10.1017/S2040618500035668CrossRefGoogle Scholar
Sandier, E. and Serfaty, S., ‘From the Ginzburg–Landau model to vortex lattice problems’, Comm. Math. Phys. 313(3) (2012), 635–743.10.1007/s00220-012-1508-xCrossRefGoogle Scholar
Sarnak, P. and Strömbergsson, A., ‘Minima of Epstein’s zeta function and heights of flat tori’, Invent. Math. 165 (2006), 115–151.10.1007/s00222-005-0488-2CrossRefGoogle Scholar
Serfaty, S., ‘Systems of points with Coulomb interactions’, EMS Newsl. 12 (2018), 16–21.10.4171/NEWS/110/6CrossRefGoogle Scholar
Ventevogel, W. J., ‘On the configuration of systems of interacting particle with minimum potential energy per particle’, Physica A 92(3–4) (1978), 343–361.10.1016/0378-4371(78)90136-XCrossRefGoogle Scholar