No CrossRef data available.
Article contents
ON A CONJECTURE ON SHIFTED PRIMES WITH LARGE PRIME FACTORS, II
Published online by Cambridge University Press: 13 September 2024
Abstract
Let 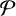 $\mathcal {P}$ be the set of primes and
$\mathcal {P}$ be the set of primes and 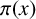 $\pi (x)$ the number of primes not exceeding x. Let
$\pi (x)$ the number of primes not exceeding x. Let 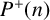 $P^+(n)$ be the largest prime factor of n, with the convention
$P^+(n)$ be the largest prime factor of n, with the convention 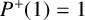 $P^+(1)=1$, and
$P^+(1)=1$, and 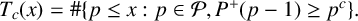 $ T_c(x)=\#\{p\le x:p\in \mathcal {P},P^+(p-1)\ge p^c\}. $ Motivated by a conjecture of Chen and Chen [‘On the largest prime factor of shifted primes’, Acta Math. Sin. (Engl. Ser.) 33 (2017), 377–382], we show that for any c with
$ T_c(x)=\#\{p\le x:p\in \mathcal {P},P^+(p-1)\ge p^c\}. $ Motivated by a conjecture of Chen and Chen [‘On the largest prime factor of shifted primes’, Acta Math. Sin. (Engl. Ser.) 33 (2017), 377–382], we show that for any c with 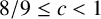 $8/9\le c<1$,
$8/9\le c<1$,
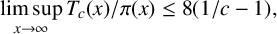 $$ \begin{align*} \limsup_{x\rightarrow\infty}T_c(x)/\pi(x)\le 8(1/c-1), \end{align*} $$
$$ \begin{align*} \limsup_{x\rightarrow\infty}T_c(x)/\pi(x)\le 8(1/c-1), \end{align*} $$which clearly means that
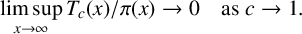 $$ \begin{align*} \limsup_{x\rightarrow\infty}T_c(x)/\pi(x)\rightarrow 0 \quad \text{as } c\rightarrow 1. \end{align*} $$
$$ \begin{align*} \limsup_{x\rightarrow\infty}T_c(x)/\pi(x)\rightarrow 0 \quad \text{as } c\rightarrow 1. \end{align*} $$Keywords
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 111 , Issue 1 , February 2025 , pp. 48 - 55
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The author is supported by National Natural Science Foundation of China (Grant No. 12201544), Natural Science Foundation of Jiangsu Province, China (Grant No. BK20210784) and China Postdoctoral Science Foundation (Grant No. 2022M710121).



