Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cusick, T. W.
and
Krass, S.
1988.
Formulas for some diophantine approximation constants.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 44,
Issue. 3,
p.
311.
Burger, Edward B
2000.
On Simultaneous Diophantine Approximation in the Vector Space Q+Qα.
Journal of Number Theory,
Vol. 82,
Issue. 1,
p.
12.


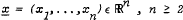 , and any ε > 0 there exist
, and any ε > 0 there exist 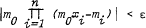 . In this paper we show this conjecture holds for all
. In this paper we show this conjecture holds for all 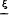 = (ξ
= (ξ