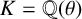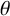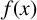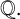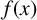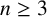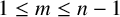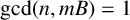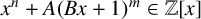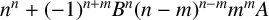1 Introduction and statements of results
Let
![]() $K={\mathbb {Q}}(\theta )$
be an algebraic number field and let
$K={\mathbb {Q}}(\theta )$
be an algebraic number field and let
![]() $f(x)$
of degree n be the minimal polynomial of
$f(x)$
of degree n be the minimal polynomial of
![]() $\theta $
over
$\theta $
over
![]() ${\mathbb {Q}}$
. The polynomial
${\mathbb {Q}}$
. The polynomial
![]() $f(x)$
is said to be monogenic if
$f(x)$
is said to be monogenic if
![]() $\{1,\theta ,\ldots ,\theta ^{n-1}\}$
is an integral basis of K.
$\{1,\theta ,\ldots ,\theta ^{n-1}\}$
is an integral basis of K.
Denote the ring of algebraic integers of K by
![]() ${\mathbb {Z}}_K$
. The field K is said to be monogenic if there exists
${\mathbb {Z}}_K$
. The field K is said to be monogenic if there exists
![]() $\alpha \in {\mathbb {Z}}_K$
such that
$\alpha \in {\mathbb {Z}}_K$
such that
![]() ${\mathbb {Z}}_K={\mathbb {Z}}[\alpha ].$
It is well known that if
${\mathbb {Z}}_K={\mathbb {Z}}[\alpha ].$
It is well known that if
![]() $f(x)$
is monogenic, then the number field K is monogenic but the converse is not always true (for example,
$f(x)$
is monogenic, then the number field K is monogenic but the converse is not always true (for example,
![]() ${\mathbb {Q}}(\sqrt {d}),$
where
${\mathbb {Q}}(\sqrt {d}),$
where
![]() $d\ne 1$
is a square-free integer congruent to
$d\ne 1$
is a square-free integer congruent to
![]() $1$
modulo
$1$
modulo
![]() $4$
).
$4$
).
The discriminant of a monic polynomial over a field
![]() $\mathbb {F}$
of degree n having roots
$\mathbb {F}$
of degree n having roots
![]() $\theta _1, \ldots , \theta _n$
in the algebraic closure of
$\theta _1, \ldots , \theta _n$
in the algebraic closure of
![]() $\mathbb {F}$
is
$\mathbb {F}$
is
![]() $\Delta _f=\prod _{1\leq i<j\leq n}^{}(\theta _i-\theta _j)^2.$
It is a classical result in algebraic number theory that if
$\Delta _f=\prod _{1\leq i<j\leq n}^{}(\theta _i-\theta _j)^2.$
It is a classical result in algebraic number theory that if
![]() $f(x)$
is the minimal polynomial of an algebraic integer
$f(x)$
is the minimal polynomial of an algebraic integer
![]() $\theta $
over
$\theta $
over
![]() ${\mathbb {Q}}$
, then the discriminant
${\mathbb {Q}}$
, then the discriminant
![]() $ \Delta _f$
of
$ \Delta _f$
of
![]() $f(x)$
and the discriminant
$f(x)$
and the discriminant
![]() $d_K$
of
$d_K$
of
![]() $K={\mathbb {Q}}(\theta )$
are related by the formula
$K={\mathbb {Q}}(\theta )$
are related by the formula
Clearly if
![]() $\Delta_f$
is square-free, then
$\Delta_f$
is square-free, then
![]() $f(x)$
is monogenic but the converse need not be true. Jones [Reference Jones4, Reference Jones6] constructed infinite families of monogenic polynomials having non square-free discriminant. In [Reference Jones7], Jones showed that there exist infinitely many primes
$f(x)$
is monogenic but the converse need not be true. Jones [Reference Jones4, Reference Jones6] constructed infinite families of monogenic polynomials having non square-free discriminant. In [Reference Jones7], Jones showed that there exist infinitely many primes
![]() $p \kern1.3pt{\geq }\kern1.3pt 3$
and integers
$p \kern1.3pt{\geq }\kern1.3pt 3$
and integers
![]() $t \kern1.4pt{\geq}\kern1.4pt 1$
coprime to p, such that
$t \kern1.4pt{\geq}\kern1.4pt 1$
coprime to p, such that
![]() ${f(x) \kern1.3pt{=}\kern1.3pt x^p \kern1.3pt{-}\kern1.3pt 2ptx^{p-1} \kern1.3pt{+}\kern1.3pt p^2t^2x^{p-2} \kern1.3pt{+}\kern1.3pt 1}$
is nonmonogenic and, in [Reference Jones5], he gave infinite families of monogenic polynomials using a new discriminant formula.
${f(x) \kern1.3pt{=}\kern1.3pt x^p \kern1.3pt{-}\kern1.3pt 2ptx^{p-1} \kern1.3pt{+}\kern1.3pt p^2t^2x^{p-2} \kern1.3pt{+}\kern1.3pt 1}$
is nonmonogenic and, in [Reference Jones5], he gave infinite families of monogenic polynomials using a new discriminant formula.
Throughout the paper,
![]() $f(x)=x^n+A(Bx+1)^m\in {\mathbb {Z}}[x]$
is an irreducible polynomial with
$f(x)=x^n+A(Bx+1)^m\in {\mathbb {Z}}[x]$
is an irreducible polynomial with
![]() $n\ge 3$
and
$n\ge 3$
and
![]() $1\le m\le n-1$
,
$1\le m\le n-1$
,
![]() $\theta $
is a root of f,
$\theta $
is a root of f,
![]() $K={\mathbb {Q}}(\theta )$
is the corresponding algebraic number field,
$K={\mathbb {Q}}(\theta )$
is the corresponding algebraic number field,
![]() $\Delta _f$
denotes the discriminant of
$\Delta _f$
denotes the discriminant of
![]() $f(x)$
and
$f(x)$
and
![]() $\mathrm {Ind}_K(\theta )$
denotes the group index
$\mathrm {Ind}_K(\theta )$
denotes the group index
![]() $ [{\mathbb {Z}}_K: {\mathbb {Z}}[\theta ]]$
. From [Reference Jones4, Theorem 3.1],
$ [{\mathbb {Z}}_K: {\mathbb {Z}}[\theta ]]$
. From [Reference Jones4, Theorem 3.1],
Theorem 1.1. Let
![]() $A,B,n,m$
be integers with
$A,B,n,m$
be integers with
![]() $1\le m\le n-1, n> 2$
and
$1\le m\le n-1, n> 2$
and
![]() $B\ne 0.$
Assume that
$B\ne 0.$
Assume that
![]() $\gcd (n,mB)=1.$
Then an irreducible polynomial of the type
$\gcd (n,mB)=1.$
Then an irreducible polynomial of the type
![]() $f(x)=x^n+A (Bx+1)^m$
is monogenic if and only if both A and
$f(x)=x^n+A (Bx+1)^m$
is monogenic if and only if both A and
![]() $n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA$
are square-free.
$n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA$
are square-free.
Remark 1.2. In Theorem 1.1, the assumption that
![]() $\gcd (n,mB)=1$
cannot be dropped. For example, consider the polynomial
$\gcd (n,mB)=1$
cannot be dropped. For example, consider the polynomial
![]() $f(x){\kern-1pt}={\kern-1pt}x^3{\kern-1pt}-{\kern-1pt}6(3x+{\kern-1pt}1)$
. Here
$f(x){\kern-1pt}={\kern-1pt}x^3{\kern-1pt}-{\kern-1pt}6(3x+{\kern-1pt}1)$
. Here
![]() $n{\kern-1pt}={\kern-1pt}3, m{\kern-1pt}={\kern-1pt}1, A{\kern-1pt}={\kern-1pt}-6$
and
$n{\kern-1pt}={\kern-1pt}3, m{\kern-1pt}={\kern-1pt}1, A{\kern-1pt}={\kern-1pt}-6$
and
![]() $B=3.$
Note that
$B=3.$
Note that
![]() $f(x)$
is irreducible over
$f(x)$
is irreducible over
![]() ${\mathbb {Q}}.$
The polynomial
${\mathbb {Q}}.$
The polynomial
![]() $f(x)$
is monogenic and has discriminant
$f(x)$
is monogenic and has discriminant
![]() $\Delta _f=23.2^2.3^5.$
However,
$\Delta _f=23.2^2.3^5.$
However,
![]() $n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA=23.3^3$
is not square-free.
$n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA=23.3^3$
is not square-free.
The following corollary is an immediate consequence of Theorem 1.1. It is conjectured by Jones in [Reference Jones4, Conjecture 4.1].
Corollary 1.3. Let p be a prime number, and
![]() $n, m$
and B be positive integers with
$n, m$
and B be positive integers with
![]() $1\le m\le n-1,~n>2$
and
$1\le m\le n-1,~n>2$
and
![]() $\gcd (n,mB)=1.$
Then
$\gcd (n,mB)=1.$
Then
![]() $f(x)=x^n+p(Bx+1)^m$
is monogenic if and only if
$f(x)=x^n+p(Bx+1)^m$
is monogenic if and only if
![]() $n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mp$
is square-free.
$n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mp$
is square-free.
Example 1.4. Let p be an odd prime number and let
![]() $a,b$
be positive integers with
$a,b$
be positive integers with
![]() $n>2$
. Consider the polynomial
$n>2$
. Consider the polynomial
![]() $f(x)=x^n+ax^2+bx+p$
with
$f(x)=x^n+ax^2+bx+p$
with
![]() $b^2=4ap.$
Note that
$b^2=4ap.$
Note that
![]() $f(x)$
satisfies Eisenstein’s criterion with respect to p, so it is irreducible over
$f(x)$
satisfies Eisenstein’s criterion with respect to p, so it is irreducible over
![]() ${\mathbb {Q}}$
. The polynomial
${\mathbb {Q}}$
. The polynomial
![]() $x^n+ax^2+bx+p$
with
$x^n+ax^2+bx+p$
with
![]() $b^2=4ap$
can be reduced to the form
$b^2=4ap$
can be reduced to the form
![]() $x^n+p(Bx+1)^2$
with
$x^n+p(Bx+1)^2$
with
![]() $B={b}/{2p}.$
If
$B={b}/{2p}.$
If
![]() $\gcd (n,2B)=1,$
that is,
$\gcd (n,2B)=1,$
that is,
![]() $\gcd (n,{b}/{p})=1,$
then Corollary 1.3 implies that
$\gcd (n,{b}/{p})=1,$
then Corollary 1.3 implies that
![]() $f(x)$
is monogenic if and only if
$f(x)$
is monogenic if and only if
![]() $n^n+(-1)^n4({b}/{2p})^n({n-2})^{n-2}p$
is square-free.
$n^n+(-1)^n4({b}/{2p})^n({n-2})^{n-2}p$
is square-free.
Example 1.5. Let B be an integer not divisible by
![]() $3$
with
$3$
with
![]() $|B|\ge 4$
and let
$|B|\ge 4$
and let
![]() $A\neq \pm 1$
be a nonzero square-free integer. Then the polynomial
$A\neq \pm 1$
be a nonzero square-free integer. Then the polynomial
![]() $f(x)=x^3+A(Bx+1)^2$
is irreducible by Perron’s criterion, which states that if
$f(x)=x^3+A(Bx+1)^2$
is irreducible by Perron’s criterion, which states that if
![]() ${f(x)=x^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0\in {\mathbb {Z}}[x]}$
with
${f(x)=x^n+a_{n-1}x^{n-1}+\cdots +a_1x+a_0\in {\mathbb {Z}}[x]}$
with
![]() $a_0\ne 0 \hspace {0.1in} \text {and}~ \hspace {0.1in} |a_{n-1}|>1+|a_{n-2}|+\cdots +|a_0|,$
then the polynomial
$a_0\ne 0 \hspace {0.1in} \text {and}~ \hspace {0.1in} |a_{n-1}|>1+|a_{n-2}|+\cdots +|a_0|,$
then the polynomial
![]() $f(x)$
is irreducible over
$f(x)$
is irreducible over
![]() $\mathbb {Q}$
. In view of Theorem 1.1, the polynomial
$\mathbb {Q}$
. In view of Theorem 1.1, the polynomial
![]() $x^3+A(Bx+1)^2$
is monogenic if and only if
$x^3+A(Bx+1)^2$
is monogenic if and only if
![]() $4AB^3-27$
is square-free.
$4AB^3-27$
is square-free.
2 Preliminary results
In what follows, for a prime number p and a given polynomial
![]() $g(x) \in {\mathbb {Z}}[x],~ \overline{g} (x)$
will denote the polynomial obtained by reducing each coefficient of
$g(x) \in {\mathbb {Z}}[x],~ \overline{g} (x)$
will denote the polynomial obtained by reducing each coefficient of
![]() $ g(x)$
modulo
$ g(x)$
modulo
![]() $p $
.
$p $
.
Let
![]() $f(x)\in {\mathbb {Z}}[x]$
be a monic irreducible polynomial having a root
$f(x)\in {\mathbb {Z}}[x]$
be a monic irreducible polynomial having a root
![]() $\theta $
and let
$\theta $
and let
![]() $L={\mathbb {Q}}(\theta )$
be an algebraic number field. In 1878, Dedekind proved the following criterion which gives a necessary and sufficient condition to be satisfied by
$L={\mathbb {Q}}(\theta )$
be an algebraic number field. In 1878, Dedekind proved the following criterion which gives a necessary and sufficient condition to be satisfied by
![]() $f(x)$
so that p does not divide
$f(x)$
so that p does not divide
![]() $\mathrm {Ind}_L(\theta )$
.
$\mathrm {Ind}_L(\theta )$
.
Theorem 2.1 (Dedekind’s criterion, [Reference Dedekind2]; see also [Reference Cohen1, Theorem 6.1.4]).
Let
![]() $L=\mathbb {Q}(\theta )$
be an algebraic number field and
$L=\mathbb {Q}(\theta )$
be an algebraic number field and
![]() $f(x)$
the minimal polynomial of the algebraic integer
$f(x)$
the minimal polynomial of the algebraic integer
![]() $\theta $
over
$\theta $
over
![]() $\mathbb {Q}.$
Let p be a prime and
$\mathbb {Q}.$
Let p be a prime and
![]() $\overline {f}(x) = \overline {g}_{1}(x)^{e_{1}}\cdots \overline {g}_{t}(x)^{e_{t}}$
be the factorisation of
$\overline {f}(x) = \overline {g}_{1}(x)^{e_{1}}\cdots \overline {g}_{t}(x)^{e_{t}}$
be the factorisation of
![]() $\overline {f}(x)$
as a product of powers of distinct irreducible polynomials over
$\overline {f}(x)$
as a product of powers of distinct irreducible polynomials over
![]() $\mathbb {Z}/p\mathbb {Z},$
with each
$\mathbb {Z}/p\mathbb {Z},$
with each
![]() $g_{i}(x)\in \mathbb {Z}[x]$
monic. Let
$g_{i}(x)\in \mathbb {Z}[x]$
monic. Let
![]() $M(x) = (f(x)-g_{1}(x)^{e_{1}}\cdots g_{t}(x)^{e_{t}})/p \in \mathbb {Z}[x]$
. Then p does not divide
$M(x) = (f(x)-g_{1}(x)^{e_{1}}\cdots g_{t}(x)^{e_{t}})/p \in \mathbb {Z}[x]$
. Then p does not divide
![]() $\mathrm {Ind}_L(\theta )$
if and only if, for each i, either
$\mathrm {Ind}_L(\theta )$
if and only if, for each i, either
![]() $e_{i}=1$
or
$e_{i}=1$
or
![]() $ \overline{g}_{i}(x)$
does not divide
$ \overline{g}_{i}(x)$
does not divide
![]() $\overline {M}(x).$
$\overline {M}(x).$
With the notation as in Theorem 2.1, one can easily check that if
![]() $f(x)$
is monogenic, then for each prime p dividing
$f(x)$
is monogenic, then for each prime p dividing
![]() $\Delta _f$
, either
$\Delta _f$
, either
![]() $e_i=1$
or
$e_i=1$
or
![]() $ \overline{g}_i(x)$
does not divide
$ \overline{g}_i(x)$
does not divide
![]() $\overline {M}(x)$
for each i.
$\overline {M}(x)$
for each i.
Definition 2.2. A polynomial
![]() $a_nx^n+a_{n-1}x^{n-1}+\cdots +a_0$
in
$a_nx^n+a_{n-1}x^{n-1}+\cdots +a_0$
in
![]() ${\mathbb {Z}}[x]$
with
${\mathbb {Z}}[x]$
with
![]() $a_n\ne 0$
is called an Eisenstein polynomial with respect to a prime p if
$a_n\ne 0$
is called an Eisenstein polynomial with respect to a prime p if
![]() $p\nmid a_n,$
$p\nmid a_n,$
![]() $p\mid a_i$
for
$p\mid a_i$
for
![]() $0\le i\le n-1$
and
$0\le i\le n-1$
and
![]() $p^2\nmid a_0.$
$p^2\nmid a_0.$
The following result is known as Eisenstein’s criterion (see [Reference Ireland and Rosen3]). It will be used in the proof of Corollary 1.3.
Theorem 2.3. Let
![]() $g(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_0\in {\mathbb {Z}}[x]$
with
$g(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_0\in {\mathbb {Z}}[x]$
with
![]() $n\ge 1.$
If there is a prime number p such that
$n\ge 1.$
If there is a prime number p such that
![]() $ p\nmid a_n, p\mid a_{n-1},\ldots , p\mid a_0$
and
$ p\nmid a_n, p\mid a_{n-1},\ldots , p\mid a_0$
and
![]() $p^2\nmid a_0,$
then
$p^2\nmid a_0,$
then
![]() $g(x)$
is irreducible over
$g(x)$
is irreducible over
![]() ${\mathbb {Q}}$
.
${\mathbb {Q}}$
.
The following lemma will be used in the proof of Theorem 1.1.
Lemma 2.4 [Reference Narkiewicz8, Lemma 2.17].
Let
![]() $\alpha $
be an algebraic integer and let
$\alpha $
be an algebraic integer and let
![]() $L={\mathbb {Q}}(\alpha )$
. If the minimal polynomial of
$L={\mathbb {Q}}(\alpha )$
. If the minimal polynomial of
![]() $\alpha $
over
$\alpha $
over
![]() ${\mathbb {Q}}$
is an Eisenstein polynomial with respect to the prime
${\mathbb {Q}}$
is an Eisenstein polynomial with respect to the prime
![]() $p,$
then
$p,$
then
![]() $\mathrm {Ind}_L(\alpha )$
is not divisible by
$\mathrm {Ind}_L(\alpha )$
is not divisible by
![]() $p.$
$p.$
3 Proof of Theorem 1.1 and Corollary 1.3
Proof of Theorem 1.1.
Clearly
![]() $A\ne 0.$
Suppose that
$A\ne 0.$
Suppose that
![]() $\theta $
is a root of
$\theta $
is a root of
![]() $f(x)$
and
$f(x)$
and
![]() $K={\mathbb {Q}}(\theta )$
. From (1.2),
$K={\mathbb {Q}}(\theta )$
. From (1.2),
First suppose that the polynomial
![]() $f(x)$
is monogenic. Then
$f(x)$
is monogenic. Then
![]() $\mathrm {Ind}_K(\theta )=1.$
Let p be a prime dividing
$\mathrm {Ind}_K(\theta )=1.$
Let p be a prime dividing
![]() $\Delta _f$
. The following cases arise.
$\Delta _f$
. The following cases arise.
Case 1:
![]() $p\mid A$
. Then
$p\mid A$
. Then
![]() $f(x)\equiv x^n\,\mod p$
and
$f(x)\equiv x^n\,\mod p$
and
![]() $M(x)=A(Bx+1)^m/p$
. As
$M(x)=A(Bx+1)^m/p$
. As
![]() $n\ge 3$
, by Dedekind’s criterion, we see that
$n\ge 3$
, by Dedekind’s criterion, we see that
![]() $\overline{x}$
should not divide
$\overline{x}$
should not divide
![]() $\overline {M}(x).$
This implies that
$\overline {M}(x).$
This implies that
![]() $p^2\nmid A.$
Thus, A is square-free. Suppose that
$p^2\nmid A.$
Thus, A is square-free. Suppose that
![]() $p^2$
divides
$p^2$
divides
![]() $(n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA).$
Then the hypothesis
$(n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA).$
Then the hypothesis
![]() $p\mid A$
implies that
$p\mid A$
implies that
![]() $p\mid n.$
Since
$p\mid n.$
Since
![]() $n\ge 3$
and A is square-free, we have
$n\ge 3$
and A is square-free, we have
![]() $p\mid B^n(n-m)^{n-m}m^m,$
that is,
$p\mid B^n(n-m)^{n-m}m^m,$
that is,
![]() $p\mid m(n-m)B,$
which is not true because
$p\mid m(n-m)B,$
which is not true because
![]() $\gcd (n,mB)= 1.$
It follows that
$\gcd (n,mB)= 1.$
It follows that
![]() $p^2$
cannot divide
$p^2$
cannot divide
![]() $(n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA)$
and so
$(n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA)$
and so
![]() $ (n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA)$
is square-free.
$ (n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA)$
is square-free.
Case 2:
![]() $p\nmid A$
. Then p will divide
$p\nmid A$
. Then p will divide
![]() $(n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA).$
Keeping in mind the hypothesis
$(n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA).$
Keeping in mind the hypothesis
![]() $\gcd (n,mB)=1,$
it is easy to see that
$\gcd (n,mB)=1,$
it is easy to see that
![]() $p\nmid n$
and so
$p\nmid n$
and so
![]() $p\nmid Bm(n-m)$
. Let
$p\nmid Bm(n-m)$
. Let
![]() $\alpha $
be a repeated root of
$\alpha $
be a repeated root of
![]() $\overline{f}(x)=x^n+\overline{A}(\overline{B}x+1)^m$
in the algebraic closure of
$\overline{f}(x)=x^n+\overline{A}(\overline{B}x+1)^m$
in the algebraic closure of
![]() ${\mathbb {Z}}/p{\mathbb {Z}}.$
Then
${\mathbb {Z}}/p{\mathbb {Z}}.$
Then
and
So
![]() $n\alpha ^{n-1}\equiv -mAB(B\alpha +1)^{m-1}\,\mod p.$
By substitution,
$n\alpha ^{n-1}\equiv -mAB(B\alpha +1)^{m-1}\,\mod p.$
By substitution,
that is,
If
![]() $B\alpha +1\equiv 0\,\mod p,$
then
$B\alpha +1\equiv 0\,\mod p,$
then
![]() $\alpha \equiv -{1}/{B}\,\mod p,$
which yields the contradiction
$\alpha \equiv -{1}/{B}\,\mod p,$
which yields the contradiction
![]() ${(-1)^n}/{\overline {B}^n}=\overline {f}({-1}//{\overline {B}})=\overline {f}(\overline {\alpha })=0.$
Thus,
${(-1)^n}/{\overline {B}^n}=\overline {f}({-1}//{\overline {B}})=\overline {f}(\overline {\alpha })=0.$
Thus,
![]() $\alpha AB(n-m)+nA\equiv 0\,\mod p,$
so that
$\alpha AB(n-m)+nA\equiv 0\,\mod p,$
so that
is the unique repeated root of
![]() $\overline {f}(x)$
in
$\overline {f}(x)$
in
![]() ${\mathbb {Z}}/p{\mathbb {Z}}$
and it is easy to show that
${\mathbb {Z}}/p{\mathbb {Z}}$
and it is easy to show that
![]() $\alpha $
has multiplicity
$\alpha $
has multiplicity
![]() $2.$
So, assuming that
$2.$
So, assuming that
![]() $\alpha $
is a positive integer satisfying (3.1), we can write
$\alpha $
is a positive integer satisfying (3.1), we can write
 $$ \begin{align*} f(x) & =(x-\alpha+\alpha)^n+A(B(x-\alpha+\alpha)+1)^m,\\ & =\displaystyle\sum_{k=0}^{n}\binom{n}{k}\alpha^{n-k}(x-\alpha)^k+A\bigg(\displaystyle\sum_{k=0}^{m}\binom{m}{k}(B\alpha+1)^{m-k}B^k(x-\alpha)^k\bigg),\\ & =(x-\alpha)^2h(x)+f'(\alpha)(x-\alpha)+f(\alpha), \end{align*} $$
$$ \begin{align*} f(x) & =(x-\alpha+\alpha)^n+A(B(x-\alpha+\alpha)+1)^m,\\ & =\displaystyle\sum_{k=0}^{n}\binom{n}{k}\alpha^{n-k}(x-\alpha)^k+A\bigg(\displaystyle\sum_{k=0}^{m}\binom{m}{k}(B\alpha+1)^{m-k}B^k(x-\alpha)^k\bigg),\\ & =(x-\alpha)^2h(x)+f'(\alpha)(x-\alpha)+f(\alpha), \end{align*} $$
where
![]() $f'(x)$
is the derivative of
$f'(x)$
is the derivative of
![]() $f(x)$
and
$f(x)$
and
 $$ \begin{align*}h(x)=\displaystyle\sum_{k=2}^{n}\binom{n}{k}\alpha^{n-k}(x-\alpha)^{k-2}+A\bigg(\displaystyle\sum_{k=2}^{m}\binom{m}{k}(B\alpha+1)^{m-k}B^k(x-\alpha)^{k-2}\bigg)\end{align*} $$
$$ \begin{align*}h(x)=\displaystyle\sum_{k=2}^{n}\binom{n}{k}\alpha^{n-k}(x-\alpha)^{k-2}+A\bigg(\displaystyle\sum_{k=2}^{m}\binom{m}{k}(B\alpha+1)^{m-k}B^k(x-\alpha)^{k-2}\bigg)\end{align*} $$
is in
![]() ${\mathbb {Z}}[x].$
Then
${\mathbb {Z}}[x].$
Then
![]() $\overline {f}(x)=(x-\overline {\alpha })^2\overline {h}(x),$
where
$\overline {f}(x)=(x-\overline {\alpha })^2\overline {h}(x),$
where
![]() $\overline {h}(x)\in {\mathbb {Z}}[x]$
is separable. Let
$\overline {h}(x)\in {\mathbb {Z}}[x]$
is separable. Let
![]() $\prod _{i=1}^{t} \overline{h}_i(x)$
be the factorisation of
$\prod _{i=1}^{t} \overline{h}_i(x)$
be the factorisation of
![]() $\overline {h}(x)$
into a product of distinct irreducible polynomials
$\overline {h}(x)$
into a product of distinct irreducible polynomials
![]() $\overline {h}_i(x)\in {\mathbb {Z}}/p{\mathbb {Z}}[x]$
with each
$\overline {h}_i(x)\in {\mathbb {Z}}/p{\mathbb {Z}}[x]$
with each
![]() $h_i(x)\in {\mathbb {Z}}[x]$
monic. Then we can write
$h_i(x)\in {\mathbb {Z}}[x]$
monic. Then we can write
 $$ \begin{align*} f(x)=(x-\alpha)^2\bigg(\displaystyle\prod_{i=1}^{t}h_i(x)+p g(x)\bigg)+f'(\alpha)(x-\alpha)+f(\alpha), \end{align*} $$
$$ \begin{align*} f(x)=(x-\alpha)^2\bigg(\displaystyle\prod_{i=1}^{t}h_i(x)+p g(x)\bigg)+f'(\alpha)(x-\alpha)+f(\alpha), \end{align*} $$
for some polynomial
![]() $g(x)\in {\mathbb {Z}}[x]$
. This implies that
$g(x)\in {\mathbb {Z}}[x]$
. This implies that
 $$ \begin{align*}M(x)=\frac{1}{p}[p (x-\alpha)^2g(x)+(x-\alpha)f'(\alpha)+f(\alpha)].\end{align*} $$
$$ \begin{align*}M(x)=\frac{1}{p}[p (x-\alpha)^2g(x)+(x-\alpha)f'(\alpha)+f(\alpha)].\end{align*} $$
In view of Dedekind’s criterion and the hypothesis that
![]() $f(x)$
is monogenic, we see that
$f(x)$
is monogenic, we see that
![]() $f(\alpha )\not \equiv 0\,\mod p^2.$
Equivalently,
$f(\alpha )\not \equiv 0\,\mod p^2.$
Equivalently,
Hence,
![]() $(n^n+(-1)^{n+m}(n-m)^{n-m}m^mB^nA)$
is square-free.
$(n^n+(-1)^{n+m}(n-m)^{n-m}m^mB^nA)$
is square-free.
Conversely, suppose A and
![]() $(n^n+(-1)^{n+m}(n-m)^{n-m}m^mB^nA)$
are square-free. If
$(n^n+(-1)^{n+m}(n-m)^{n-m}m^mB^nA)$
are square-free. If
![]() $A=\pm 1,$
then using (1.1), we see that
$A=\pm 1,$
then using (1.1), we see that
![]() $\mathrm {Ind}_K(\theta )=1,$
that is,
$\mathrm {Ind}_K(\theta )=1,$
that is,
![]() $f(x)$
is monogenic. If p be a prime divisor of
$f(x)$
is monogenic. If p be a prime divisor of
![]() $A,$
then
$A,$
then
![]() $f(x)$
is an Eisenstein polynomial with respect to the prime p. Therefore, by Lemma 2.4,
$f(x)$
is an Eisenstein polynomial with respect to the prime p. Therefore, by Lemma 2.4,
![]() $p\nmid \mathrm {Ind}_K(\theta ).$
Hence, by (1.1),
$p\nmid \mathrm {Ind}_K(\theta ).$
Hence, by (1.1),
![]() $f(x)$
is monogenic. This completes the proof of the theorem.
$f(x)$
is monogenic. This completes the proof of the theorem.