No CrossRef data available.
Article contents
On a class of finite soluble groups
Published online by Cambridge University Press: 17 April 2009
Abstract
Let the group T be the direct product of groups Si (i = 1, … r) where for a given group Ai, Si is the direct product of ni factors Ai × Ai × … × Ai. Let B be a group that has a faithful permutation representation Γi of degree ni. (i = 1, …, r). Consider G, the split extension of T by B defined by letting B act on T as follows.
Each Si is normal in G. If 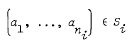 and b ∈ B then
and b ∈ B then 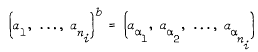 where
where  . It is proved that if T is an M-group and all subgroups of B are M-groups, then G is an M-group. This is a generalisation of a result of Gary M. Seitz, Math. Z. 110 (1969), 101–122, who proved the particular case where r = 1 and Γ1 is the regular representation of B.
. It is proved that if T is an M-group and all subgroups of B are M-groups, then G is an M-group. This is a generalisation of a result of Gary M. Seitz, Math. Z. 110 (1969), 101–122, who proved the particular case where r = 1 and Γ1 is the regular representation of B.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1975


