Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T15:07:30.897Z Has data issue: false hasContentIssue false
  • English
  • Français

On a class of differential equations which model tide-well systems

Published online by Cambridge University Press:  17 April 2009

B. J. Noye
B. J. Noye
Affiliation:
University of Adelaide, Adelaide, South Australia.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For three possible types of tide-well systems the non-dimensional head response, Y(τ), to a sinusoidal fluctuation of the sea-level is given by the differential equation 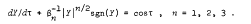Estimates of the non-dimensional well response Z(τ) = sinτ - Y(τ) are found by considering the steady state solutions of the above equation. With n = 2 the equation is linear and an exact solution can be found; for n ≠ 2 the equation is non-linear and several methods which give approximate solutions are described. The methods used can be extended to cover other values of n; for example, with n = 4 the equation corresponds to one governing oscillations near resonance in open pipes.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 3 , Issue 3 , December 1970 , pp. 391 - 411
Copyright
Copyright © Australian Mathematical Society 1970

References

[1]Keulegan, G.H., Tidal flow in entrances; water level fluctuations of basins in communication with seas (Technical Bulletin no. 14, U.S. Army Corps of Engineers, Committee on Tidal Hydraulics, 1967).Google Scholar
[2]Noye, B.J., “The frequency response of a tide-well”, Proc. 3rd Aust. Conf. on Hydraulics and Fluid Mechanics, Sydney, 1968, 65–71.Google Scholar
[3]Shipley, A.M., “On measuring long waves with a tide gauge”, Deutsche Hydrographische Zeitschrift 16 (1963), 136–140.CrossRefGoogle Scholar
[4]van Dyke, M., “Perturbation methods in fluid mechanics”, Applied Mathematics and Mechanics, 8 (Academic Press, New York, London, 1964).Google Scholar
[5]van Wijngaarden, L., “On the oscillations near and at resonance in open pipes”, J. Engrg. Math. 2 (1968), 225–240.CrossRefGoogle Scholar