Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T23:16:41.175Z Has data issue: false hasContentIssue false
  • English
  • Français

On a centre-like subset of a ring without nil ideals

Published online by Cambridge University Press:  17 April 2009

Itzhak Nada
Itzhak Nada
Affiliation:
Department of Mathematical Sciences, Tel-Aviv University, Tel-Aviv, Israel
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a new proof of the hypercentre theorem of Herstein.

In [1], Herstein has defined the hypercentre of a ring R as follows:

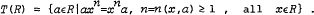
Herstein has proved:

THEOREM. If R is a ring without non-zero nil ideals, thenT (R) = Z (R).

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 34 , Issue 1 , August 1986 , pp. 149 - 151
Copyright
Copyright © Australian Mathematical Society 1986

References

[1]Herstein, I.N., “On the hypercentre of a ring”, J. Algebra 36 (1975), 151–157.CrossRefGoogle Scholar
[2]Herstein, I.N., “Invariant subrings of a certain kind”, Israel J. Math. 26 (1977), 205–208.CrossRefGoogle Scholar
[3]Herstein, I.N., “Two remarks on commutativity of rings”, Canad. J. Math. 7 (1955), 411–412.CrossRefGoogle Scholar
[4]Chacron, M., “Algebraic φ-rings extensions of bounded index,” J. Algebra 44 (1977), 370–388.CrossRefGoogle Scholar