No CrossRef data available.
Article contents
ON 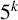 $5^k$-REGULAR PARTITIONS MODULO POWERS OF
$5^k$-REGULAR PARTITIONS MODULO POWERS OF 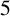 $5$
$5$
Published online by Cambridge University Press: 14 April 2025
Abstract
In this work, we investigate the arithmetic properties of 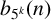 $b_{5^k}(n)$, which counts the partitions of n where no part is divisible by
$b_{5^k}(n)$, which counts the partitions of n where no part is divisible by 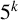 $5^k$. By constructing generating functions for
$5^k$. By constructing generating functions for 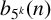 $b_{5^k}(n)$ across specific arithmetic progressions, we establish a set of Ramanujan-type congruences.
$b_{5^k}(n)$ across specific arithmetic progressions, we establish a set of Ramanujan-type congruences.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Hirschhorn, M. D. and Hunt, D. C., ‘A simple proof of the Ramanujan conjecture for powers of 5’, J. reine angew. Math. 326 (1981), 1–17.Google Scholar
Ramanujan, S., Collected Papers of Srinivasa Ramanujan (eds. Hardy, G. H., Seshu Aiyar, P. V. and Wilson, B. M.) (AMS Chelsea Publishing, Providence, RI, 2000).Google Scholar
Ranganatha, D., ‘Ramanujan-type congruences modulo powers of 5 and 7’, Indian J. Pure Appl. Math. 48 (2017), 449–465.CrossRefGoogle Scholar
Wang, L., ‘Congruences for
 $5$
-regular partitions modulo powers of
$5$
-regular partitions modulo powers of
 $5$
’, Ramanujan J. 44 (2017), 343–358.Google Scholar
$5$
’, Ramanujan J. 44 (2017), 343–358.Google Scholar
Watson, G. N., ‘Ramanujans Vermutung über Zerfällungsanzahlen’, J. reine angew. Math. 179 (1938), 97–128.CrossRefGoogle Scholar



