Published online by Cambridge University Press: 17 April 2009
Recently, B.-Y. Chen obtained an inequality for slant surfaces in complex space forms. Further, B.-Y. Chen and one of the present authors proved the non-minimality of proper slant surfaces in non-flat complex space forms. In the present paper, we investigate 3-dimensional proper contact slant submanifolds in Sasakian space forms. A sharp inequality is obtained between the scalar curvature (intrinsic invariant) and the main extrinsic invariant, namely the squared mean curvature.
It is also shown that a 3-dimensional contact slant submanifold M of a Sasakian space form 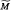 (c), with c ≠ 1, cannot be minimal.
(c), with c ≠ 1, cannot be minimal.