Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T01:05:01.992Z Has data issue: false hasContentIssue false
  • English
  • Français

OBSERVATIONS ON GAUSSIAN UPPER BOUNDS FOR NEUMANN HEAT KERNELS

Part of: Parabolic equations and systems

Published online by Cambridge University Press:  08 July 2015

MOURAD CHOULLI ,
LAURENT KAYSER  and
EL MAATI OUHABAZ
MOURAD CHOULLI*
Affiliation:
Institut Élie Cartan de Lorraine, UMR CNRS 7502, Université de Lorraine, Boulevard des Aiguillettes, BP 70239, 54506 Vandoeuvre les Nancy cedex - Ile du Saulcy, 57045 Metz cedex 01, France email [email protected]
LAURENT KAYSER
Affiliation:
Institut Élie Cartan de Lorraine, UMR CNRS 7502, Université de Lorraine, Boulevard des Aiguillettes, BP 70239, 54506 Vandoeuvre les Nancy cedex - Ile du Saulcy, 57045 Metz cedex 01, France email [email protected]
EL MAATI OUHABAZ
Affiliation:
Institut Mathématiques de Bordeaux, UMR CNRS 5251, Université de Bordeaux, 351 Cours de la Libération, F-33405 Talence, France email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Given a domain 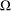${\rm\Omega}$ of a complete Riemannian manifold 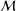${\mathcal{M}}$, define 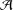${\mathcal{A}}$ to be the Laplacian with Neumann boundary condition on 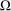${\rm\Omega}$. We prove that, under appropriate conditions, the corresponding heat kernel satisfies the Gaussian upper bound

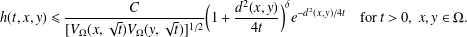$$\begin{eqnarray}h(t,x,y)\leq \frac{C}{[V_{{\rm\Omega}}(x,\sqrt{t})V_{{\rm\Omega}}(y,\sqrt{t})]^{1/2}}\biggl(1+\frac{d^{2}(x,y)}{4t}\biggr)^{{\it\delta}}e^{-d^{2}(x,y)/4t}\quad \text{for}~t>0,~x,y\in {\rm\Omega}.\end{eqnarray}$$
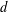Here $d$ is the geodesic distance on 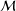${\mathcal{M}}$, 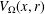$V_{{\rm\Omega}}(x,r)$ is the Riemannian volume of 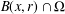$B(x,r)\cap {\rm\Omega}$, where 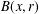$B(x,r)$ is the geodesic ball of centre $x$ and radius $r$, and 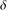${\it\delta}$ is a constant related to the doubling property of 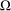${\rm\Omega}$. As a consequence we obtain analyticity of the semigroup 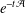$e^{-t{\mathcal{A}}}$ on 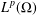$L^{p}({\rm\Omega})$ for all 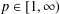$p\in [1,\infty )$ as well as a spectral multiplier result.

Keywords

heat kernelsGaussian boundsNeumann LaplacianRiemannian manifolds

MSC classification

Primary: 35K08: Heat kernel
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 92 , Issue 3 , December 2015 , pp. 429 - 439
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Boutayeb, S., Coulhon, T. and Sikora, A., ‘A new approach to pointwise heat kernel upper bounds on doubling metric measure spaces’, Adv. Math. 270 (2015), 302–374.CrossRefGoogle Scholar
Choulli, M. and Kayser, L., ‘Gaussian lower bound for the Neumann Green function of a general parabolic operator’, Positivity, doi:10.1007/s11117-014-0319-z.CrossRefGoogle Scholar
Coulhon, T. and Sikora, A., ‘Gaussian heat kernel bounds via Phragmèn–Lindelöf theorem’, Proc. Lond. Math. Soc. (3) 96(3) (2008), 507–544.CrossRefGoogle Scholar
Davies, E. B., One-Parameter Semigroups (Academic, London, 1980).Google Scholar
Davies, E. B., Heat Kernels and Spectral Theory, Cambridge Tracts in Mathematics, 92 (Cambridge University Press, London, 1989).CrossRefGoogle Scholar
Davies, E. B., ‘L p spectral independence and L 1 analyticity’, J. Lond. Math. Soc. (2) 52(2) (1995), 177–184.CrossRefGoogle Scholar
Duong, X. T., Ouhabaz, E. M. and Sikora, A., ‘Plancherel-type estimates and sharp spectral multipliers’, J. Funct. Anal. 196 (2002), 443–485.CrossRefGoogle Scholar
Gyrya, P. and Saloff-Coste, L., ‘Neumann and Dirichlet heat kernels in inner uniform domains’, Astérisque (No. 336) (2011).Google Scholar
Henrot, A. and Pierre, M., Variation et optimisation de formes, Mathématiques et Applications, 48 (Springer, Berlin, 2005).CrossRefGoogle Scholar
Kloeckner, B. R. and Kuperberg, G., ‘A refinement of Günther’s candle inequality’, Preprint, 2012, arXiv:1204.3943.Google Scholar
Li, P. and Yau, S.T., ‘On the parabolic kernel of the Schrödinger operator’, Acta Math. 156 (1986), 153–201.CrossRefGoogle Scholar
Mitrea, D., Mitrea, M. and Shaw, M. C., ‘Traces of differential forms on Lipschitz domains, the boundary De Rham complex, and Hodge decompositions’, Preprint.Google Scholar
Ouhabaz, E. M., ‘Gaussian estimates and holomorphy of semigroups’, Proc. Amer. Math. Soc. 123(5) (1995), 1465–1474.CrossRefGoogle Scholar
Ouhabaz, E. M., Analysis of Heat Equations on Domains, London Mathematical Society Monographs, 31 (Princeton University Press, Princeton, NJ, 2004).Google Scholar
Saloff-Coste, L., ‘Pseudo-Poincaré inequalities and applications to Sobolev inequalities’, in: Around the Research of Vladimir Maz’ya. I, International Mathematical Series (New York), 11 (Springer, New York, 2010), 349–372.CrossRefGoogle Scholar