1 Introduction
Let
![]() $\mathrm {M}_d(\cdot )$
denote the set of
$\mathrm {M}_d(\cdot )$
denote the set of
![]() $d \times d$
matrices with entries in the set
$d \times d$
matrices with entries in the set
![]() $\mathbb {Z}$
of integers or the set
$\mathbb {Z}$
of integers or the set
![]() $\mathbb {Q}$
of rational numbers, as indicated. Every (additive) subsemigroup of
$\mathbb {Q}$
of rational numbers, as indicated. Every (additive) subsemigroup of
![]() $\mathbb {N} = \{0,1,2,\ldots \}$
is the exponent semigroup
$\mathbb {N} = \{0,1,2,\ldots \}$
is the exponent semigroup
of some
![]() $A \in \mathrm {M}_d(\mathbb {Q})$
by [Reference Chhabra, Garcia, Zhang and Zhang6, Corollary 6.5]. In particular, every numerical semigroup S, that is, a subsemigroup of
$A \in \mathrm {M}_d(\mathbb {Q})$
by [Reference Chhabra, Garcia, Zhang and Zhang6, Corollary 6.5]. In particular, every numerical semigroup S, that is, a subsemigroup of
![]() $\mathbb {N}$
with finite complement [Reference Assi, D’Anna and García-Sánchez3, Reference Rosales and García-Sánchez15], is of the form
$\mathbb {N}$
with finite complement [Reference Assi, D’Anna and García-Sánchez3, Reference Rosales and García-Sánchez15], is of the form
![]() $S = \mathcal {S}(A)$
with
$S = \mathcal {S}(A)$
with
![]() $A \in \mathrm {M}_c(\mathbb {Q})$
, in which
$A \in \mathrm {M}_c(\mathbb {Q})$
, in which
![]() $c=c(S) = 1 + \max (\mathbb {N} \backslash S)$
is the conductor of S [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2]. This ensures that the matricial dimension
$c=c(S) = 1 + \max (\mathbb {N} \backslash S)$
is the conductor of S [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2]. This ensures that the matricial dimension
of a numerical semigroup
![]() $S \subseteq \mathbb {N}$
is well defined and
$S \subseteq \mathbb {N}$
is well defined and
![]() $\operatorname {dim}_{\mathrm {mat}} S \leq c(S)$
.
$\operatorname {dim}_{\mathrm {mat}} S \leq c(S)$
.
Each numerical semigroup S has a unique minimal system of generators, that is, positive
![]() $n_1 < n_2 < \cdots < n_k$
such that
$n_1 < n_2 < \cdots < n_k$
such that
![]() $S = \langle n_1,n_2,\ldots ,n_k \rangle $
is the smallest additive subsemigroup of
$S = \langle n_1,n_2,\ldots ,n_k \rangle $
is the smallest additive subsemigroup of
![]() $\mathbb {N}$
containing
$\mathbb {N}$
containing
![]() $n_1, n_2,\ldots , n_k$
. Here,
$n_1, n_2,\ldots , n_k$
. Here,
![]() $e(S) = k$
is the embedding dimension of S and
$e(S) = k$
is the embedding dimension of S and
![]() $m(S) = n_1$
is the multiplicity of S.
$m(S) = n_1$
is the multiplicity of S.
The main result of this paper is the following dramatic improvement of [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2], in which
![]() $m(S) = n_1$
replaces
$m(S) = n_1$
replaces
![]() $c(S)$
.
$c(S)$
.
Theorem 1.1. If S is a nontrivial numerical semigroup with multiplicity (minimal generator)
![]() $m(S)$
, there is an
$m(S)$
, there is an
![]() $A \in \mathrm {M}_{m(S)}(\mathbb {Q})$
such that
$A \in \mathrm {M}_{m(S)}(\mathbb {Q})$
such that
![]() $\mathcal {S}(A) = S$
. Thus,
$\mathcal {S}(A) = S$
. Thus,
![]() $\operatorname {dim}_{\mathrm {mat}} S \leq m(S)$
.
$\operatorname {dim}_{\mathrm {mat}} S \leq m(S)$
.
Theorem 1.1 gives an explicit construction in terms of Apéry sets [Reference Apéry2], a mainstay in the study of numerical semigroups [Reference Rosales12, Reference Wilf17]. At the core of the proof lies a system of inequalities that reflect the fine structure of Apéry sets; these were first introduced by Kunz in [Reference Kunz11], and have since been used in enumerative [Reference Alhajjar, Russell and Steward1, Reference Kaplan8, Reference Rosales, García-Sánchez, García-García and Branco16] and classification [Reference Elmacioglu, Hilmer, O’Neill, Okandan and Park-Kaufmann7, Reference Kaplan and O’Neill9] problems in this area.
This paper is organised as follows. Section 2 contains the proof of Theorem 1.1. Section 3 presents several illustrative examples and Corollary 3.6, which extends Theorem 1.1 to arbitrary semigroups in
![]() $\mathbb {N}$
. We close by computing the matricial dimension for irreducible numerical semigroups in Section 4.
$\mathbb {N}$
. We close by computing the matricial dimension for irreducible numerical semigroups in Section 4.
2 Proof of Theorem 1.1
This section contains the proof of Theorem 1.1 and some preliminary remarks. Recall that the Apéry set of a numerical semigroup S with multiplicity m is the set
Each element of
![]() $\operatorname {Ap}(S)$
is the smallest element of S in its equivalence class modulo m, so one often writes
$\operatorname {Ap}(S)$
is the smallest element of S in its equivalence class modulo m, so one often writes
in which
![]() $a_0 = 0$
and each
$a_0 = 0$
and each
![]() $a_i \equiv i \bmod m$
. It is convenient to interpret the subscripts of the
$a_i \equiv i \bmod m$
. It is convenient to interpret the subscripts of the
![]() $a_i$
modulo m. For example, it was shown by Kunz in [Reference Kunz11] that
$a_i$
modulo m. For example, it was shown by Kunz in [Reference Kunz11] that
and that this system of inequalities (along with the modular requirements and minimality of m) characterise Apéry sets of numerical semigroups.
Before proceeding to the proof of Theorem 1.1, let us first illustrate the matricial structure employed in the proof. Suppose
![]() $z_0,z_1,z_2,z_3 \neq 0$
and
$z_0,z_1,z_2,z_3 \neq 0$
and
 $$ \begin{align*} A = \begin{bmatrix} {\color{lightgray}0} & z_1 & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & z_2 & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & z_3 \\ z_0 & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix} \in \mathrm{M}_4(\mathbb{Q}), \end{align*} $$
$$ \begin{align*} A = \begin{bmatrix} {\color{lightgray}0} & z_1 & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & z_2 & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & z_3 \\ z_0 & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix} \in \mathrm{M}_4(\mathbb{Q}), \end{align*} $$
which is a generalised permutation matrix or, equivalently, the adjacency matrix of a weighted directed cycle graph on four vertices. Observe that
 $$ \begin{align*} A^{4q} &= \left[ \begin{smallmatrix} (z_0 z_1 z_2 z_3)^{q} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & (z_0 z_1 z_2 z_3)^{q} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & (z_0 z_1 z_2 z_3)^{q} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & (z_0 z_1 z_2 z_3)^{q} \\ \end{smallmatrix}\right],\\ A^{4q+1} &= \left[\begin{smallmatrix} {\color{lightgray}0} & z_1 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & z_2 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & z_3 (z_0 z_1 z_2 z_3)^q \\ z_0 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{smallmatrix}\right],\\ A^{4q+2} &= \left[\begin{smallmatrix} {\color{lightgray}0} & {\color{lightgray}0} & z_1 z_2 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & z_2 z_3 (z_0 z_1 z_2 z_3)^q \\ z_3 z_0 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & z_0 z_1 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{smallmatrix}\right] \quad \text{and}\\ A^{4q+3} &= \left[\begin{smallmatrix} {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & z_1 z_2 z_3 (z_0 z_1 z_2 z_3)^q \\ z_3 z_0 z_2 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & z_3 z_0 z_1 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & z_0 z_1 z_2 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} \\ \end{smallmatrix}\right]. \end{align*} $$
$$ \begin{align*} A^{4q} &= \left[ \begin{smallmatrix} (z_0 z_1 z_2 z_3)^{q} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & (z_0 z_1 z_2 z_3)^{q} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & (z_0 z_1 z_2 z_3)^{q} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & (z_0 z_1 z_2 z_3)^{q} \\ \end{smallmatrix}\right],\\ A^{4q+1} &= \left[\begin{smallmatrix} {\color{lightgray}0} & z_1 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & z_2 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & z_3 (z_0 z_1 z_2 z_3)^q \\ z_0 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{smallmatrix}\right],\\ A^{4q+2} &= \left[\begin{smallmatrix} {\color{lightgray}0} & {\color{lightgray}0} & z_1 z_2 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & z_2 z_3 (z_0 z_1 z_2 z_3)^q \\ z_3 z_0 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & z_0 z_1 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{smallmatrix}\right] \quad \text{and}\\ A^{4q+3} &= \left[\begin{smallmatrix} {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & z_1 z_2 z_3 (z_0 z_1 z_2 z_3)^q \\ z_3 z_0 z_2 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & z_3 z_0 z_1 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & z_0 z_1 z_2 (z_0 z_1 z_2 z_3)^q & {\color{lightgray}0} \\ \end{smallmatrix}\right]. \end{align*} $$
Writing
![]() $p = 4q+r$
, with
$p = 4q+r$
, with
![]() $q, r \in \mathbb {Z}$
and
$q, r \in \mathbb {Z}$
and
![]() $0 \leq r \leq 3$
, the nonzero entries of
$0 \leq r \leq 3$
, the nonzero entries of
![]() $A^p$
are
$A^p$
are
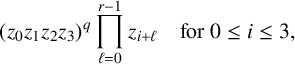 $$ \begin{align} (z_0 z_1 z_2 z_3)^q \prod_{\ell = 0}^{r - 1} z_{i + \ell} \quad \text{for } 0 \leq i \leq 3, \end{align} $$
$$ \begin{align} (z_0 z_1 z_2 z_3)^q \prod_{\ell = 0}^{r - 1} z_{i + \ell} \quad \text{for } 0 \leq i \leq 3, \end{align} $$
in which the subscripts are interpreted modulo m.
For the proof of Theorem 1.1, we generalise (2.2) to the
![]() $m \times m$
setting, and let each
$m \times m$
setting, and let each
![]() $z_i$
take the form
$z_i$
take the form
![]() $b^{x_i}$
with
$b^{x_i}$
with
![]() $b \in \mathbb {Z} \backslash \{-1,0,1\}$
and
$b \in \mathbb {Z} \backslash \{-1,0,1\}$
and
![]() $x_i \in \mathbb {Z}$
, so that the multiplicative structure of (2.2) becomes additive.
$x_i \in \mathbb {Z}$
, so that the multiplicative structure of (2.2) becomes additive.
Proof of Theorem 1.1.
Suppose S is a numerical semigroup with multiplicity
![]() $m \geq 2$
and Apéry set
$m \geq 2$
and Apéry set
![]() $\operatorname {Ap}(S) = \{a_0, a_1, \ldots , a_{m-1}\}$
, in which
$\operatorname {Ap}(S) = \{a_0, a_1, \ldots , a_{m-1}\}$
, in which
![]() $a_0 = 0$
and
$a_0 = 0$
and
![]() $a_i \equiv i \,(\operatorname {mod} m)$
for each i. For each
$a_i \equiv i \,(\operatorname {mod} m)$
for each i. For each
![]() $i = 0, 1, \ldots , m-1$
, let
$i = 0, 1, \ldots , m-1$
, let
where the subscripts of the
![]() $x_i$
are, like those of the
$x_i$
are, like those of the
![]() $a_i$
, interpreted modulo m. Notice that each
$a_i$
, interpreted modulo m. Notice that each
![]() $x_i \in \mathbb {Z}$
since
$x_i \in \mathbb {Z}$
since
![]() $a_{i-1} - a_i + 1 \equiv 0 \,(\operatorname {mod} m)$
, and telescoping yields
$a_{i-1} - a_i + 1 \equiv 0 \,(\operatorname {mod} m)$
, and telescoping yields
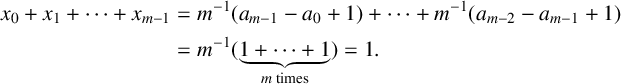 $$ \begin{align} x_0+ x_1 + \cdots + x_{m-1} &= {m^{-1}}(a_{m-1} - a_0 + 1) + \cdots + {m^{-1}}(a_{m-2} - a_{m-1} + 1) \nonumber \\ &= {m^{-1}}(\underbrace{1 + \cdots + 1}_{m \text{ times}}) = 1. \end{align} $$
$$ \begin{align} x_0+ x_1 + \cdots + x_{m-1} &= {m^{-1}}(a_{m-1} - a_0 + 1) + \cdots + {m^{-1}}(a_{m-2} - a_{m-1} + 1) \nonumber \\ &= {m^{-1}}(\underbrace{1 + \cdots + 1}_{m \text{ times}}) = 1. \end{align} $$
Fix a base
![]() $b \in \mathbb {Z} \backslash \{-1,0,1\}$
and let
$b \in \mathbb {Z} \backslash \{-1,0,1\}$
and let
![]() $A \in \mathrm {M}_m(\mathbb {Q})$
denote the matrix
$A \in \mathrm {M}_m(\mathbb {Q})$
denote the matrix
 $$ \begin{align} A = \begin{bmatrix} {\color{lightgray}0} & b^{x_1} & {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & b^{x_2} & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & b^{x_3} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\ddots & \color{lightgray}\vdots \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & b^{x_{m-1}} \\ b^{x_0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \end{bmatrix}. \end{align} $$
$$ \begin{align} A = \begin{bmatrix} {\color{lightgray}0} & b^{x_1} & {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & b^{x_2} & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & b^{x_3} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\ddots & \color{lightgray}\vdots \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & b^{x_{m-1}} \\ b^{x_0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \end{bmatrix}. \end{align} $$
By (2.2), for each
![]() $p \geq 0$
, writing
$p \geq 0$
, writing
![]() $p = qm + r$
with
$p = qm + r$
with
![]() $q, r \in \mathbb {Z}$
and
$q, r \in \mathbb {Z}$
and
![]() $0 \le r \le m-1$
, the exponent of b in each nonzero entry of
$0 \le r \le m-1$
, the exponent of b in each nonzero entry of
![]() $A^p$
has the form
$A^p$
has the form
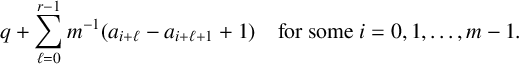 $$ \begin{align*} q + \sum_{\ell = 0}^{r-1} {m^{-1}}(a_{i+\ell} - a_{i+\ell+1} + 1) \quad \text{for some } i = 0, 1, \ldots, m-1. \end{align*} $$
$$ \begin{align*} q + \sum_{\ell = 0}^{r-1} {m^{-1}}(a_{i+\ell} - a_{i+\ell+1} + 1) \quad \text{for some } i = 0, 1, \ldots, m-1. \end{align*} $$
As such, to prove
![]() $\mathcal {S}(A) = S$
, we must show that the condition
$\mathcal {S}(A) = S$
, we must show that the condition
holds if and only if
![]() $p \in \mathcal {S}(A)$
. This clearly holds whenever
$p \in \mathcal {S}(A)$
. This clearly holds whenever
![]() $m \mid p$
since in this case,
$m \mid p$
since in this case,
![]() $r = 0$
and
$r = 0$
and
![]() $q \geq 0$
. By the definition of the Apéry set, it suffices to prove that for each
$q \geq 0$
. By the definition of the Apéry set, it suffices to prove that for each
![]() $j = 1, \ldots , m-1$
, we have
$j = 1, \ldots , m-1$
, we have
-
(a)
 $a_j \in \mathcal {S}(A)$
and
$a_j \in \mathcal {S}(A)$
and -
(b)
 $a_j - m \notin \mathcal {S}(A)$
.
$a_j - m \notin \mathcal {S}(A)$
.
Indeed, if
![]() $p = a_j$
, then for each
$p = a_j$
, then for each
![]() $i = 0, 1, \ldots , m-1$
, (2.5) becomes
$i = 0, 1, \ldots , m-1$
, (2.5) becomes
wherein nonnegativity follows from (2.1). Additionally, if
![]() $p = a_j - m$
, then choosing
$p = a_j - m$
, then choosing
![]() $i = 0$
,
$i = 0$
,
so condition (2.5) does not hold. This completes the proof.
3 Examples and remarks
This section contains several remarks and illustrative examples of Theorem 1.1 that demonstrate the effectiveness of our main result, along with an extension of Theorem 1.1 to arbitrary subsemigroups of
![]() $\mathbb {N}$
. We begin with a careful analysis of how things play out for the so-called McNugget semigroup.
$\mathbb {N}$
. We begin with a careful analysis of how things play out for the so-called McNugget semigroup.
Example 3.1. Consider
![]() $S = \langle 6,9,20 \rangle $
. Then,
$S = \langle 6,9,20 \rangle $
. Then,
![]() $m(S) = 6$
and
$m(S) = 6$
and
![]() $c(S) = 44$
, so the construction of [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2] produces a
$c(S) = 44$
, so the construction of [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2] produces a
![]() $B \in \mathrm {M}_{44}(\mathbb {Q})$
such that
$B \in \mathrm {M}_{44}(\mathbb {Q})$
such that
![]() $\mathcal {S}(B) = S$
. In contrast, Theorem 1.1 produces an
$\mathcal {S}(B) = S$
. In contrast, Theorem 1.1 produces an
![]() $A \in \mathrm {M}_6(\mathbb {Q})$
such that
$A \in \mathrm {M}_6(\mathbb {Q})$
such that
![]() $\mathcal {S}(A) = S$
. Indeed, one can check that
$\mathcal {S}(A) = S$
. Indeed, one can check that
![]() $\operatorname {Ap}(S) = \{0, 49, 20, 9, 40, 29\}$
, so the proof of Theorem 1.1 yields
$\operatorname {Ap}(S) = \{0, 49, 20, 9, 40, 29\}$
, so the proof of Theorem 1.1 yields
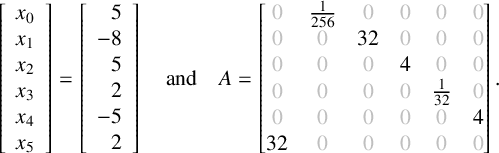 $$ \begin{align*} \left[ \begin{array}{r} x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ \end{array} \right] = \left[ \begin{array}{r} 5 \\ -8 \\ 5 \\ 2 \\ -5 \\ 2 \\ \end{array} \right] \quad \text{and} \quad A= \begin{bmatrix} {\color{lightgray}0} & \frac{1}{256} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & 32 & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & 4 & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \frac{1}{32} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & 4 \\ 32 & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix}. \end{align*} $$
$$ \begin{align*} \left[ \begin{array}{r} x_0 \\ x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ \end{array} \right] = \left[ \begin{array}{r} 5 \\ -8 \\ 5 \\ 2 \\ -5 \\ 2 \\ \end{array} \right] \quad \text{and} \quad A= \begin{bmatrix} {\color{lightgray}0} & \frac{1}{256} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & 32 & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & 4 & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \frac{1}{32} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & 4 \\ 32 & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix}. \end{align*} $$
In fact, this establishes
![]() $\operatorname {dim}_{\mathrm {mat}} S = 6$
by Corollary 4.2 below.
$\operatorname {dim}_{\mathrm {mat}} S = 6$
by Corollary 4.2 below.
Example 3.2. If
![]() $S = \langle 5, 11 \rangle $
, then
$S = \langle 5, 11 \rangle $
, then
![]() $\operatorname {Ap}(S) = \{0, 11, 22, 33, 44\}$
, so Theorem 1.1 yields
$\operatorname {Ap}(S) = \{0, 11, 22, 33, 44\}$
, so Theorem 1.1 yields
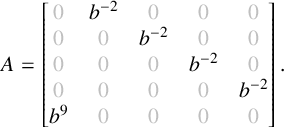 $$ \begin{align*} A = \begin{bmatrix} {\color{lightgray}0} & b^{-2} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & b^{-2} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & b^{-2} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & b^{-2} \\ b^{9} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix}. \end{align*} $$
$$ \begin{align*} A = \begin{bmatrix} {\color{lightgray}0} & b^{-2} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & b^{-2} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & b^{-2} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & b^{-2} \\ b^{9} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix}. \end{align*} $$
More generally, if
![]() $S = \langle m, km + 1 \rangle $
with
$S = \langle m, km + 1 \rangle $
with
![]() $k \in \mathbb {N}$
, then
$k \in \mathbb {N}$
, then
![]() $\operatorname {Ap}(S)$
comprises integer multiples of
$\operatorname {Ap}(S)$
comprises integer multiples of
![]() $km + 1$
, so
$km + 1$
, so
![]() $a_i = i(km + 1)$
for
$a_i = i(km + 1)$
for
![]() $i = 1,2,\ldots ,m-1$
. The only nonzero integral entry of the resulting matrix is in the lower-left corner; the remaining nonzero entries are identical to each other.
$i = 1,2,\ldots ,m-1$
. The only nonzero integral entry of the resulting matrix is in the lower-left corner; the remaining nonzero entries are identical to each other.
Remark 3.3. The values of
![]() $x_0,x_1, \ldots , x_{m-1}$
in the proof of Theorem 1.1 can also be expressed in terms of the so-called Kunz coordinates
$x_0,x_1, \ldots , x_{m-1}$
in the proof of Theorem 1.1 can also be expressed in terms of the so-called Kunz coordinates
![]() $(k_1, k_2,\ldots , k_{m-1})$
of S, which are defined so that
$(k_1, k_2,\ldots , k_{m-1})$
of S, which are defined so that
![]() $a_i = k_im + i$
for each
$a_i = k_im + i$
for each
![]() $i = 1,2, \ldots , m-1$
[Reference Kunz11]. In particular,
$i = 1,2, \ldots , m-1$
[Reference Kunz11]. In particular,
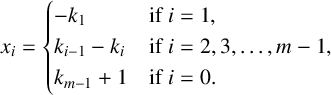 $$ \begin{align*} x_i = \begin{cases} -k_1 & \text{if } i = 1, \\ k_{i-1} - k_i & \text{if } i = 2,3, \ldots, m-1, \\ k_{m-1} + 1 & \text{if } i = 0. \end{cases} \end{align*} $$
$$ \begin{align*} x_i = \begin{cases} -k_1 & \text{if } i = 1, \\ k_{i-1} - k_i & \text{if } i = 2,3, \ldots, m-1, \\ k_{m-1} + 1 & \text{if } i = 0. \end{cases} \end{align*} $$
Translating (2.1) in terms of Kunz coordinates requires the use of cases; this motivates the choice of expression for
![]() $x_i$
in the proof of Theorem 1.1.
$x_i$
in the proof of Theorem 1.1.
Remark 3.4. The parameter
![]() $b \in \mathbb {Z} \backslash \{-1,0,1\}$
in the proof of Theorem 1.1 is arbitrary. Laplace (cofactor) expansion of (2.4) and using (2.3) ensure that
$b \in \mathbb {Z} \backslash \{-1,0,1\}$
in the proof of Theorem 1.1 is arbitrary. Laplace (cofactor) expansion of (2.4) and using (2.3) ensure that
![]() $\det A = (-1)^{m-1}b$
, so
$\det A = (-1)^{m-1}b$
, so
![]() $\det A$
is arbitrary in
$\det A$
is arbitrary in
![]() $\mathbb {Z} \backslash \{-1,0,1\}$
and essentially independent of S. However,
$\mathbb {Z} \backslash \{-1,0,1\}$
and essentially independent of S. However,
![]() $\det A = \pm 1$
implies that S is cyclic [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 4.2]. Moreover,
$\det A = \pm 1$
implies that S is cyclic [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 4.2]. Moreover,
![]() $\det A = 0$
whenever A is nilpotent, and [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2] ensures that every numerical semigroup is the exponent semigroup of a nilpotent matrix.
$\det A = 0$
whenever A is nilpotent, and [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2] ensures that every numerical semigroup is the exponent semigroup of a nilpotent matrix.
Example 3.5. A small adjustment to the proof of Theorem 1.1 permits one to find a representing matrix for any given subsemigroup of
![]() $\mathbb {N}$
, numerical or not. Let us consider
$\mathbb {N}$
, numerical or not. Let us consider
![]() $S = \langle 6,8,10 \rangle $
. Since
$S = \langle 6,8,10 \rangle $
. Since
![]() $S = 2T$
, in which
$S = 2T$
, in which
![]() $T = \langle 3,7,11 \rangle $
is a numerical semigroup, we have
$T = \langle 3,7,11 \rangle $
is a numerical semigroup, we have
![]() $T = \mathcal {S}(A)$
and
$T = \mathcal {S}(A)$
and
![]() $S = \mathcal {S}(B)$
for
$S = \mathcal {S}(B)$
for
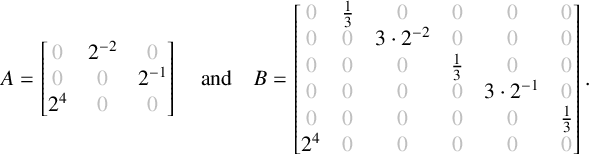 $$ \begin{align*} A = \begin{bmatrix} {\color{lightgray}0} & 2^{-2} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & 2^{-1} \\ 2^4 & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix} \quad \text{and} \quad B = \begin{bmatrix} {\color{lightgray}0} & \frac{1}{3} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & 3 \cdot 2^{-2} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \frac{1}{3} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & 3 \cdot 2^{-1} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \frac{1}{3} \\ 2^4 & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix}. \end{align*} $$
$$ \begin{align*} A = \begin{bmatrix} {\color{lightgray}0} & 2^{-2} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & 2^{-1} \\ 2^4 & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix} \quad \text{and} \quad B = \begin{bmatrix} {\color{lightgray}0} & \frac{1}{3} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & 3 \cdot 2^{-2} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \frac{1}{3} & {\color{lightgray}0} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & 3 \cdot 2^{-1} & {\color{lightgray}0} \\ {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & \frac{1}{3} \\ 2^4 & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} & {\color{lightgray}0} \\ \end{bmatrix}. \end{align*} $$
We record this observation here.
Corollary 3.6. If
![]() $S \subseteq \mathbb {N}$
is an additive subsemigroup, then
$S \subseteq \mathbb {N}$
is an additive subsemigroup, then
![]() $\operatorname {dim}_{\mathrm {mat}} S \le \min (S \backslash \{0\})$
.
$\operatorname {dim}_{\mathrm {mat}} S \le \min (S \backslash \{0\})$
.
Proof. Suppose
![]() $S = dT$
, where T is a numerical semigroup and
$S = dT$
, where T is a numerical semigroup and
![]() $d \in \mathbb {N}$
is positive. Let
$d \in \mathbb {N}$
is positive. Let
![]() $m = m(T)$
. As in the proof of Theorem 1.1, fix
$m = m(T)$
. As in the proof of Theorem 1.1, fix
![]() $x_0, x_1, \ldots , x_{m-1} \in \mathbb {Z}$
such that
$x_0, x_1, \ldots , x_{m-1} \in \mathbb {Z}$
such that
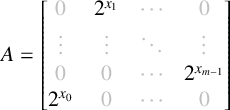 $$ \begin{align*} A = \begin{bmatrix} {\color{lightgray}0} & 2^{x_1} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\ddots & \color{lightgray}\vdots \\ {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & 2^{x_{m-1}} \\ 2^{x_0} & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \end{bmatrix} \end{align*} $$
$$ \begin{align*} A = \begin{bmatrix} {\color{lightgray}0} & 2^{x_1} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\ddots & \color{lightgray}\vdots \\ {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & 2^{x_{m-1}} \\ 2^{x_0} & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \end{bmatrix} \end{align*} $$
has
![]() $\mathcal {S}(A) = T$
. Let
$\mathcal {S}(A) = T$
. Let
![]() $B \in M_{dm}(\mathbb {Q})$
be the matrix
$B \in M_{dm}(\mathbb {Q})$
be the matrix
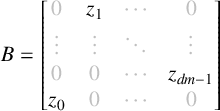 $$ \begin{align*} B = \begin{bmatrix} {\color{lightgray}0} & z_1 & \color{lightgray}\cdots & {\color{lightgray}0} \\ \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\ddots & \color{lightgray}\vdots \\ {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & z_{dm-1} \\ z_0 & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \end{bmatrix} \end{align*} $$
$$ \begin{align*} B = \begin{bmatrix} {\color{lightgray}0} & z_1 & \color{lightgray}\cdots & {\color{lightgray}0} \\ \color{lightgray}\vdots & \color{lightgray}\vdots & \color{lightgray}\ddots & \color{lightgray}\vdots \\ {\color{lightgray}0} & {\color{lightgray}0} & \color{lightgray}\cdots & z_{dm-1} \\ z_0 & {\color{lightgray}0} & \color{lightgray}\cdots & {\color{lightgray}0} \\ \end{bmatrix} \end{align*} $$
defined by
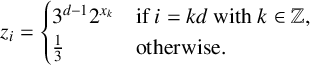 $$ \begin{align*} z_i = \begin{cases} 3^{d-1} 2^{x_k} & \text{if } i = kd \text{ with } k \in \mathbb{Z}, \\ \tfrac{1}{3} & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} z_i = \begin{cases} 3^{d-1} 2^{x_k} & \text{if } i = kd \text{ with } k \in \mathbb{Z}, \\ \tfrac{1}{3} & \text{otherwise.} \end{cases} \end{align*} $$
By (2.2), for any
![]() $p \in \mathbb {N}$
, the nonzero entries in
$p \in \mathbb {N}$
, the nonzero entries in
![]() $B^{pd}$
are precisely those that appear in
$B^{pd}$
are precisely those that appear in
![]() $A^p$
, so
$A^p$
, so
![]() $pd \in \mathcal {S}(B)$
if and only if
$pd \in \mathcal {S}(B)$
if and only if
![]() $p \in \mathcal {S}(A)$
. However, any power of B not divisible by d has at least one noninteger entry with a power of 3 in the denominator, so
$p \in \mathcal {S}(A)$
. However, any power of B not divisible by d has at least one noninteger entry with a power of 3 in the denominator, so
![]() $\gcd (\mathcal {S}(B)) = d$
. As such, we conclude
$\gcd (\mathcal {S}(B)) = d$
. As such, we conclude
![]() $\mathcal {S}(B) = S$
.
$\mathcal {S}(B) = S$
.
4 Irreducible numerical semigroups
Fix a numerical semigroup S and let
![]() $F = c(S) - 1$
. Recall that:
$F = c(S) - 1$
. Recall that:
-
(a) S is symmetric if
 $x \in \mathbb {Z} \backslash S$
implies
$x \in \mathbb {Z} \backslash S$
implies
 $F - x \in S$
;
$F - x \in S$
; -
(b) S is pseudosymmetric if F is even and
 $x \in \mathbb {Z} \backslash S$
implies
$x \in \mathbb {Z} \backslash S$
implies
 $F - x \in S$
or
$F - x \in S$
or
 $x = F/2$
;
$x = F/2$
; -
(c) S is irreducible if S cannot be written as an intersection of finitely many numerical semigroups properly containing it.
A numerical semigroup is irreducible if and only if it is symmetric or pseudosymmetric [Reference Rosales and Branco14], and these two families of numerical semigroups are each of interest in commutative algebraic settings (see [Reference Barucci, Dobbs and Fontana4, Reference Kunz10], respectively).
Remark 4.1. Every numerical semigroup can be written as an intersection of finitely many irreducible numerical semigroups, and such expressions are often far from unique [Reference Bogart and Fakhari5, Reference Rosales and Branco13]. In some cases, one can use this fact and [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 2.3(a)] to obtain a more optimal construction than Theorem 1.1. For example, Theorem 1.1 identifies
![]() $A \in \mathrm {M}_{15}(\mathbb {Q})$
with exponent semigroup
$A \in \mathrm {M}_{15}(\mathbb {Q})$
with exponent semigroup
![]() $\mathcal {S}(A) = \langle 15, 20, 21, 25, 26 \rangle $
, but
$\mathcal {S}(A) = \langle 15, 20, 21, 25, 26 \rangle $
, but
so one can obtain a block-diagonal matrix
![]() $A' \in \mathrm {M}_8(\mathbb {Q})$
with
$A' \in \mathrm {M}_8(\mathbb {Q})$
with
![]() $\mathcal {S}(A') = \mathcal {S}(A)$
by applying Theorem 1.1 to T and
$\mathcal {S}(A') = \mathcal {S}(A)$
by applying Theorem 1.1 to T and
![]() $T'$
. Note that this strategy would be ineffective with the construction in [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2] since
$T'$
. Note that this strategy would be ineffective with the construction in [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2] since
![]() $c(T \cap T') = \max (c(T), c(T'))$
, while
$c(T \cap T') = \max (c(T), c(T'))$
, while
![]() $m(T \cap T')$
can be much larger than
$m(T \cap T')$
can be much larger than
![]() $m(T) + m(T')$
.
$m(T) + m(T')$
.
Remark 4.1 does not aid in obtaining the matricial dimension of irreducible numerical semigroups, since they cannot be written as an intersection of finitely many other numerical semigroups. Luckily, Theorem 1.1 and [Reference Chhabra, Garcia, Zhang and Zhang6] together identify the matricial dimension of nearly all such semigroups. We record this here.
Corollary 4.2. If S is a symmetric numerical semigroup, then
![]() $\operatorname {dim}_{\mathrm {mat}} S = m(S)$
. In particular, if
$\operatorname {dim}_{\mathrm {mat}} S = m(S)$
. In particular, if
![]() $e(S) = 2$
, then
$e(S) = 2$
, then
![]() $\operatorname {dim}_{\mathrm {mat}} S = m(S)$
.
$\operatorname {dim}_{\mathrm {mat}} S = m(S)$
.
Proof. This follows from Theorem 1.1 since
![]() $\operatorname {dim}_{\mathrm {mat}} S \geq m(S)$
by [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 5.3]. Additionally,
$\operatorname {dim}_{\mathrm {mat}} S \geq m(S)$
by [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 5.3]. Additionally,
![]() $e(S) = 2$
implies S is symmetric by [Reference Rosales and García-Sánchez15, Corollary 4.7].
$e(S) = 2$
implies S is symmetric by [Reference Rosales and García-Sánchez15, Corollary 4.7].
Corollary 4.3. Let S be a nontrivial pseudosymmetric numerical semigroup.
-
(a) If
 $c(S) \le m(S)$
, then
$c(S) \le m(S)$
, then
 $\operatorname {dim}_{\mathrm {mat}} S = 2$
.
$\operatorname {dim}_{\mathrm {mat}} S = 2$
. -
(b) If
 $m(S) < c(S) \le 2m(S)$
, then
$m(S) < c(S) \le 2m(S)$
, then
 $m(S) - 1 \leq \operatorname {dim}_{\mathrm {mat}} S\leq m(S)$
.
$m(S) - 1 \leq \operatorname {dim}_{\mathrm {mat}} S\leq m(S)$
. -
(c) If
 $c(S)> 2m(S)$
, then
$c(S)> 2m(S)$
, then
 $\operatorname {dim}_{\mathrm {mat}} S = m(S)$
.
$\operatorname {dim}_{\mathrm {mat}} S = m(S)$
.
Proof. Combine Theorem 1.1 with the inequalities in [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 5.6].
Example 4.4. The semigroup
![]() $S = \langle 3,5,7 \rangle $
is pseudosymmetric with
$S = \langle 3,5,7 \rangle $
is pseudosymmetric with
![]() $m(S) = 3$
and
$m(S) = 3$
and
![]() $c(S) = 5$
. One can readily check that
$c(S) = 5$
. One can readily check that
![]() $\mathcal {S}(A) = S$
for
$\mathcal {S}(A) = S$
for
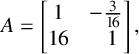 $$ \begin{align*} A = \begin{bmatrix} 1 & -\tfrac{3}{16} \\ 16 & \phantom{-}1 \end{bmatrix}, \end{align*} $$
$$ \begin{align*} A = \begin{bmatrix} 1 & -\tfrac{3}{16} \\ 16 & \phantom{-}1 \end{bmatrix}, \end{align*} $$
so
![]() $\operatorname {dim}_{\mathrm {mat}} S = 2 = m(S) - 1$
. We conjecture that
$\operatorname {dim}_{\mathrm {mat}} S = 2 = m(S) - 1$
. We conjecture that
![]() $\operatorname {dim}_{\mathrm {mat}} S = m(S) - 1$
whenever S is pseudosymmetric and
$\operatorname {dim}_{\mathrm {mat}} S = m(S) - 1$
whenever S is pseudosymmetric and
![]() $m(S) < c(S) \le 2m(S)$
.
$m(S) < c(S) \le 2m(S)$
.
Example 4.5. Consider
![]() $S = \langle 7,54,66 \rangle $
, which has
$S = \langle 7,54,66 \rangle $
, which has
![]() $m(S) = 7$
,
$m(S) = 7$
,
![]() $c(S) = 192$
and
$c(S) = 192$
and
Since S is neither symmetric or pseudosymmetric, the previous corollaries do not determine
![]() $\operatorname {dim}_{\mathrm {mat}} S$
. Theorem 1.1 ensures that
$\operatorname {dim}_{\mathrm {mat}} S$
. Theorem 1.1 ensures that
![]() $\operatorname {dim}_{\mathrm {mat}} S \leq 7$
, whereas [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2] provides the much weaker bound
$\operatorname {dim}_{\mathrm {mat}} S \leq 7$
, whereas [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 6.2] provides the much weaker bound
![]() $\operatorname {dim}_{\mathrm {mat}} S \leq 192$
. However, we can prove that
$\operatorname {dim}_{\mathrm {mat}} S \leq 192$
. However, we can prove that
![]() $\operatorname {dim}_{\mathrm {mat}} S = 7$
as follows. Suppose towards a contradiction that
$\operatorname {dim}_{\mathrm {mat}} S = 7$
as follows. Suppose towards a contradiction that
![]() $S = \mathcal {S}(A)$
, in which
$S = \mathcal {S}(A)$
, in which
![]() $A \in \mathrm {M}_d(\mathbb {Q})$
with
$A \in \mathrm {M}_d(\mathbb {Q})$
with
![]() $1 \leq d \leq 6$
. Then,
$1 \leq d \leq 6$
. Then,
![]() $185,186,187,188,189,190 \in S$
ensures that
$185,186,187,188,189,190 \in S$
ensures that
![]() $\mathcal {S}(A)$
contains all successive natural numbers [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 5.1]. This contradicts the fact that
$\mathcal {S}(A)$
contains all successive natural numbers [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 5.1]. This contradicts the fact that
![]() $c(S) - 1 = 191 \notin S$
. Therefore,
$c(S) - 1 = 191 \notin S$
. Therefore,
![]() $\operatorname {dim}_{\mathrm {mat}} S \geq 7$
, so
$\operatorname {dim}_{\mathrm {mat}} S \geq 7$
, so
![]() $\operatorname {dim}_{\mathrm {mat}} S = 7$
.
$\operatorname {dim}_{\mathrm {mat}} S = 7$
.
Example 4.6. These methods are insufficient to compute the matricial dimension of all numerical semigroups. For example, the longest string of consecutive elements in
![]() $S = \langle 39, 40, 47 \rangle $
below
$S = \langle 39, 40, 47 \rangle $
below
![]() $c(S) = 390$
is
$c(S) = 390$
is
![]() $\{351,352,\ldots ,381\}$
, which has length
$\{351,352,\ldots ,381\}$
, which has length
![]() $31$
. Thus,
$31$
. Thus,
![]() $32 \leq \operatorname {dim}_{\mathrm {mat}} S \leq 39$
by [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 5.1] and Theorem 1.1. Since S is neither symmetric nor pseudosymmetric, we cannot appeal to the corollaries above.
$32 \leq \operatorname {dim}_{\mathrm {mat}} S \leq 39$
by [Reference Chhabra, Garcia, Zhang and Zhang6, Theorem 5.1] and Theorem 1.1. Since S is neither symmetric nor pseudosymmetric, we cannot appeal to the corollaries above.



