Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-17T16:04:10.778Z Has data issue: false hasContentIssue false
  • English
  • Français

NOWHERE-ZERO 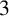$3$-FLOWS IN TWO FAMILIES OF VERTEX-TRANSITIVE GRAPHS

Part of: Graph theory

Published online by Cambridge University Press:  15 September 2022

JUNYANG ZHANG Open the ORCID record for JUNYANG ZHANG [Opens in a new window]  and
YING TAO Open the ORCID record for YING TAO [Opens in a new window]
JUNYANG ZHANG*
Affiliation:
School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, PR China
YING TAO
Affiliation:
School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 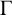$\Gamma $ be a graph of valency at least four whose automorphism group contains a minimally vertex-transitive subgroup G. It is proved that 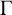$\Gamma $ admits a nowhere-zero 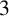$3$ -flow if one of the following two conditions holds: (i) 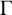$\Gamma $ is of order twice an odd number and G contains a central involution; (ii) G is a direct product of a 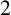$2$ -subgroup and a subgroup of odd order.

Keywords

vertex-transitive graphinteger flownowhere-zero 3-flowCayley graph

MSC classification

Primary: 05C21: Flows in graphs
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 3 , June 2023 , pp. 353 - 360
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the Basic Research and Frontier Exploration Project of Chongqing (No. cstc2018jcyjAX0010) and the Foundation of Chongqing Normal University (21XLB006).

References

Ahanjideh, M. and Iranmanesh, A., ‘The validity of Tutte’s 3-flow conjecture for some Cayley graphs’, Ars Math. Contemp. 16 (2019), 203–213.10.26493/1855-3974.1406.cc1CrossRefGoogle Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory (Springer, New York, 2008).CrossRefGoogle Scholar
Godsil, C. and Royle, G., Algebraic Graph Theory (Springer, New York, 2004).Google Scholar
Imrich, W. and Škrekovski, R., ‘A theorem on integer flows on Cartesian products of graphs’, J. Graph Theory 43 (2003), 93–98.10.1002/jgt.10100CrossRefGoogle Scholar
Jaeger, F., ‘Flows and generalized coloring theorems in graphs’, J. Combin. Theory Ser. B 26 (1979), 205–216.10.1016/0095-8956(79)90057-1CrossRefGoogle Scholar
Kochol, M., ‘An equivalent version of the 3-flow conjecture’, J. Combin. Theory Ser. B 83 (2001), 258–261.CrossRefGoogle Scholar
Li, L. and Li, X., ‘Nowhere-zero 3-flows in Cayley graphs on generalized dihedral group and generalized quaternion group’, Front. Math. China 10 (2015), 293–302.10.1007/s11464-014-0378-2CrossRefGoogle Scholar
Lovász, L. M., Thomassen, C., Wu, Y. and Zhang, C.-Q., ‘Nowhere-zero $3$ -flows and modulo $k$ -orientations’, J. Combin. Theory Ser. B 103 (2013), 587–598.10.1016/j.jctb.2013.06.003CrossRefGoogle Scholar
Mader, W., ‘Minimale $N$ -fach kantenzusammenhängende Graphen’, Math. Ann. 191 (1971), 21–28.10.1007/BF01433466CrossRefGoogle Scholar
Nánásiová, M. and Škoviera, M., ‘Nowhere-zero flows in Cayley graphs and Sylow 2-subgroups’, J. Algebraic Combin. 30 (2009), 103–110.CrossRefGoogle Scholar
Potočnik, P., Škoviera, M. and Škrekovski, R., ‘Nowhere-zero $3$ -flows in abelian Cayley graphs’, Discrete Math. 297 (2005), 119–127.10.1016/j.disc.2005.04.013CrossRefGoogle Scholar
Rotman, J. J., An Introduction to the Theory of Groups, 4th edn (Springer, New York, 1995).10.1007/978-1-4612-4176-8CrossRefGoogle Scholar
Shu, J. and Zhang, C.-Q., ‘Nowhere-zero 3-flows in products of graphs’, J. Graph Theory 50 (2005), 79–89.CrossRefGoogle Scholar
Thomassen, C., ‘The weak 3-flow conjecture and the weak circular flow conjecture’, J. Combin. Theory Ser. B 102 (2012), 521–529.10.1016/j.jctb.2011.09.003CrossRefGoogle Scholar
Yang, F. and Li, X., ‘Nowhere-zero $3$ -flows in dihedral Cayley graphs’, Inform. Process. Lett. 111 (2011), 416–419.10.1016/j.ipl.2011.01.017CrossRefGoogle Scholar
Zhang, C.-Q., Integer Flows and Cycle Covers of Graphs (Marcel Dekker Inc., New York, 1997).Google Scholar
Zhang, J. and Zhou, S., ‘Nowhere-zero 3-flows in Cayley graphs on supersolvable groups’, Preprint, 2022, arXiv:2203.02971.10.1016/j.disc.2022.113226CrossRefGoogle Scholar
Zhang, J. and Zhou, S., ‘Nowhere-zero 3-flows in nilpotently vertex-transitive graphs’, Preprint, 2022, arXiv:2203.13575.10.1017/S0004972722000922CrossRefGoogle Scholar