Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T12:56:33.188Z Has data issue: false hasContentIssue false
  • English
  • Français

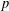A NOTE ON THE $p$-SUPERSOLUBILITY OF FINITE GROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  03 June 2016

CHANGWEN LI ,
XIAOLAN YI  and
SHOUHONG QIAO
CHANGWEN LI*
Affiliation:
School of Mathematics and Statistics, Jiangsu Normal University, Xuzhou 221116, China email [email protected]
XIAOLAN YI
Affiliation:
School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China email [email protected]
SHOUHONG QIAO
Affiliation:
School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510006, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we investigate the influence of certain subgroups of fixed prime power order on the 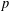$p$-supersolubility of finite groups.

Keywords

p-soluble groupp-supersoluble groupE–S-supplemented

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Secondary: 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 3 , December 2016 , pp. 431 - 436
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Ballester-Bolinches, A., Esteban-Romero, R. and Asaad, M., Products of Finite Groups (Walter de Gruyter, Berlin, 2010).Google Scholar
Ballester-Bolinches, A., Ezquerro, L. M. and Skiba, A. N., ‘Local embeddings of some families of subgroups of finite groups’, Acta Math. Sin. (Engl. Ser.) 25 (2009), 869–882.Google Scholar
Ballester-Bolinches, A. and Pedraza-Aguilera, M. C., ‘Sufficient conditions for supersolubility of finite groups’, J. Pure Appl. Algebra 127 (1998), 113–118.Google Scholar
Doerk, K. and Hawkes, T., Finite Solvable Groups (Walter de Gruyter, Berlin–New York, 1992).CrossRefGoogle Scholar
Kegel, O. H., ‘Sylow Gruppen und subnormalteiler endlicher Gruppen’, Math. Z. 78 (1962), 205–221.Google Scholar
Li, C., Yang, N. and Tang, N., ‘Some new characterizations of finite p-supersoluble groups’, Bull. Aust. Math. Soc. 89 (2014), 514–521.CrossRefGoogle Scholar
Li, C., Yu, X. and Tang, N., ‘Finite p-supersoluble groups with some E–S-supplemented subgroups’, Rend. Semin. Mat. Univ. Padova 133 (2015), 79–90.CrossRefGoogle Scholar
Li, C., Zhang, X. and Yi, X., ‘On E–S-supplemented subgroups of finite groups’, Colloq. Math. 131 (2013), 41–51.Google Scholar
Li, Y., Wang, Y. and Wei, H., ‘On p-nilpotency of finite groups with some subgroups 𝜋-quasinormally embedded’, Acta Math. Hungar. 108 (2005), 283–298.CrossRefGoogle Scholar
Schmidt, P., ‘Subgroups permutable with all Sylow subgroups’, J. Algebra 207 (1998), 285–293.Google Scholar
Skiba, A. N., ‘On weakly S-permutable subgroups of finite groups’, J. Algebra 315 (2007), 192–209.Google Scholar
Skiba, A. N., ‘A characterization of the hypercyclically embedded subgroups of finite groups’, J. Pure Appl. Algebra 215 (2011), 257–261.Google Scholar