Article contents
NOTE ON THE NUMBER OF DIVISORS OF REDUCIBLE QUADRATIC POLYNOMIALS
Published online by Cambridge University Press: 15 August 2018
Abstract
Lapkova [‘On the average number of divisors of reducible quadratic polynomials’, J. Number Theory 180 (2017), 710–729] uses a Tauberian theorem to derive an asymptotic formula for the divisor sum 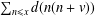 $\sum _{n\leq x}d(n(n+v))$ where
$\sum _{n\leq x}d(n(n+v))$ where  $v$ is a fixed integer and
$v$ is a fixed integer and 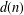 $d(n)$ denotes the number of divisors of
$d(n)$ denotes the number of divisors of  $n$. We reprove this result with additional terms in the asymptotic formula, by investigating the relationship between this divisor sum and the well-known sum
$n$. We reprove this result with additional terms in the asymptotic formula, by investigating the relationship between this divisor sum and the well-known sum 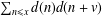 $\sum _{n\leq x}d(n)d(n+v)$.
$\sum _{n\leq x}d(n)d(n+v)$.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
Footnotes
The second author was partially supported by the Grant no. 2016/23/D/ST1/01149 from the National Science Centre.
References
- 1
- Cited by


