Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Broughan, Kevin A.
2002.
Vanishing of the integral of the Hurwitz zeta Function.
Bulletin of the Australian Mathematical Society,
Vol. 65,
Issue. 1,
p.
121.
Ashton, A. C. L.
and
Fokas, A. S.
2019.
Relations among the Riemann Zeta and Hurwitz Zeta Functions, as Well as Their Products.
Symmetry,
Vol. 11,
Issue. 6,
p.
754.
Heap, Winston
and
Sahay, Anurag
2024.
The fourth moment of the Hurwitz zeta function.
Journal für die reine und angewandte Mathematik (Crelles Journal),


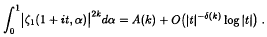
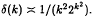 .
.