Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T05:16:53.972Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON SPECIAL VALUES OF CERTAIN DIRICHLET L-FUNCTIONS

Part of: Diophantine equations Forms and linear algebraic groups Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  13 October 2010

B. RAMAKRISHNAN
B. RAMAKRISHNAN*
Affiliation:
Harish-Chandra Research Institute, Chhatnag Road, Jhunsi, Allahabad 211 019, India (email: [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In Gun and Ramakrishnan [‘On special values of certain Dirichlet L-functions’, Ramanujan J.15 (2008), 275–280], we gave expressions for the special values of certain Dirichlet L-function in terms of finite sums involving Jacobi symbols. In this note we extend our earlier results by giving similar expressions for two more special values of Dirichlet L-functions, namely L(−1,χm) and L(−2,χ−m′), where m,m′ are square-free integers with m≡1 mod 8 and m′≡3 mod 8 and χD is the Kronecker symbol 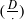. As a consequence, using the identities of Cohen [‘Sums involving the values at negative integers of L-functions of quadratic characters’, Math. Ann.217 (1975), 271–285], we also express the finite sums with Jacobi symbols in terms of sums involving divisor functions. Finally, we observe that the proof of Theorem 1.2 in Gun and Ramakrishnan (as above) is a direct consequence of Equation (24) in Gun, Manickam and Ramakrishnan [‘A canonical subspace of modular forms of half-integral weight’, Math. Ann.347 (2010), 899–916].

Keywords

Dirichlet L-functionssums of squares

MSC classification

Secondary: 11E25: Sums of squares and representations by other particular quadratic forms 11M06: $zeta (s)$ and $L(s, chi)$ 11D85: Representation problems
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 83 , Issue 3 , June 2011 , pp. 435 - 438
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

References

[1]Bateman, P. T. and Knopp, M. I., ‘Some new old-fashioned modular identities’, Ramanujan J. 2 (1998), 247–269.CrossRefGoogle Scholar
[2]Cohen, H., ‘Sums involving the values at negative integers of L-functions of quadratic characters’, Math. Ann. 217 (1975), 271–285.Google Scholar
[3]Cooper, S., ‘Sums of five, seven and nine squares’, Ramanujan J. 6 (2002), 469–490.Google Scholar
[4]Cooper, S. and Hirschhorn, M., ‘On the number of primitive representations of integers as sums of squares’, Ramanujan J. 13 (2007), 7–25.CrossRefGoogle Scholar
[5]Gun, S., Manickam, M. and Ramakrishnan, B., ‘A canonical subspace of modular forms of half-integral weight’, Math. Ann. 347 (2010), 899–916.Google Scholar
[6]Gun, S. and Ramakrishnan, B., ‘On special values of certain Dirichlet L-functions’, Ramanujan J. 15 (2008), 275–280.Google Scholar
[7]Gun, S. and Ramakrishnan, B., ‘On the representation of integers as sums of an odd number of squares’, Ramanujan J. 15 (2008), 367–376.CrossRefGoogle Scholar