Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-20T06:17:52.832Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON MÖBIUS DISJOINTNESS FOR SKEW PRODUCTS ON A CIRCLE AND A NILMANIFOLD

Part of: Exponential sums and character sums Multiplicative number theory

Published online by Cambridge University Press:  04 October 2022

XIAOGUANG HE Open the ORCID record for XIAOGUANG HE [Opens in a new window]  and
KE WANG Open the ORCID record for KE WANG [Opens in a new window]
XIAOGUANG HE*
Affiliation:
College of Mathematical Sciences, Sichuan University, Chengdu, Sichuan 610016, PR China
KE WANG
Affiliation:
Data Science Institute, Shandong University, Jinan, Shandong 250100, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 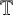$\mathbb {T}$ be the unit circle and 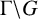${\Gamma \backslash G}$ the 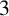$3$ -dimensional Heisenberg nilmanifold. We consider the skew products on 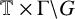$\mathbb {T} \times {\Gamma \backslash G}$ and prove that the Möbius function is linearly disjoint from these skew products which improves the recent result of Huang, Liu and Wang [‘Möbius disjointness for skew products on a circle and a nilmanifold’, Discrete Contin. Dyn. Syst. 41(8) (2021), 3531–3553].

Keywords

Möbius functiondistal flowskew productnilmanifoldmeasure complexity

MSC classification

Secondary: 11L03: Trigonometric and exponential sums, general 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 107 , Issue 3 , June 2023 , pp. 471 - 482
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is supported by the National Postdoctoral Innovative Talents Support Program (Grant No. BX20190227), the Fundamental Research Funds for the Central Universities, SCU (No. 2021SCU12109) and the National Natural Science Foundation of China (Grant No. 12101427).

References

de Faveri, A., ‘Möbius disjointness for ${C}^{1+\varepsilon }$ skew products’, Int. Math. Res. Not. IMRN 2022(4) (2022), 2513–2531.CrossRefGoogle Scholar
Ferenczi, S., Kułaga-Przymus, J. and Lemańczyk, M., ‘Sarnak’s conjecture: what’s new’, in: Ergodic Theory and Dynamical Systems in Their Interactions with Arithmetics and Combinatorics, Lecture Notes in Mathematics, 2213 (eds. Ferenczi, S., Kułaga-Przymus, J. and Lemańczyk, M.) (Springer, Cham, 2018), 163–235.10.1007/978-3-319-74908-2_11CrossRefGoogle Scholar
Furstenberg, H., ‘The structure of distal flows’, Amer. J. Math. 85 (1963), 477–515.CrossRefGoogle Scholar
Green, B. and Tao, T., ‘The quantitative behaviour of polynomial orbits on nilmanifolds’, Ann. of Math. (2) 175 (2012), 465–540.CrossRefGoogle Scholar
Green, B. and Tao, T., ‘The Möbius function is strongly orthogonal to nilsequences’, Ann. of Math. (2) 175 (2012), 541–566.CrossRefGoogle Scholar
Huang, W., Liu, J. and Wang, K., ‘Möbius disjointness for skew products on a circle and a nilmanifold’, Discrete Contin. Dyne’s. Syst. 41(8) (2021), 3531–3553.10.3934/dcds.2021006CrossRefGoogle Scholar
Huang, W., Wang, Z. and Ye, X., ‘Measure complexity and Möbius disjointness’, Adv. Math. 347 (2019), 827–858.CrossRefGoogle Scholar
Kanigowski, A., Lemańczyk, M. and Radziwiłł, M., ‘Rigidity in dynamics and Möbius disjointness’, Fund. Math. 255(3) (2021), 309–336.CrossRefGoogle Scholar
Kułaga-Przymus, J. and Lemańczyk, M., ‘The Möbius function and continuous extensions of rotations’, Monatsh. Math. 178(4) (2015), 553–582.CrossRefGoogle Scholar
Liu, J. and Sarnak, P., ‘The Möbius function and distal flows’, Duke Math. J. 164 (2015), 1353–1399.CrossRefGoogle Scholar
Parry, W., ‘Zero entropy of distal and related transformations’, in: 1968 Topological Dynamics Symposium (eds. Auslander, J. and Gottschalk, W. H.) (Colorado State University, Fort Collins, CO, 1967), 383–389.Google Scholar
Sarnak, P., Three Lectures on the Möbius Function, Randomness and Dynamics, IAS Lecture Notes, 2009; available online at https://www.math.ias.edu/files/wam/2011/PSMobius.pdf.Google Scholar
Sarnak, P., ‘Möbius randomness and dynamics’, Not. S. Afr. Math. Soc. 43 (2012), 89–97.Google Scholar
Tolimieri, R., ‘Analysis on the Heisenberg manifold’, Trans. Amer. Math. Soc. 288 (1977), 329–343.CrossRefGoogle Scholar
Wang, Y. and Yao, W., ‘Strong orthogonality between the Möbius function and skew products’, Monatsh. Math. 192(3) (2020), 745–759.CrossRefGoogle Scholar
Wang, Z., ‘Möbius disjointness for analytic skew products’, Invent. Math. 209 (2017), 175–196.CrossRefGoogle Scholar