Hostname: page-component-f554764f5-rvxtl Total loading time: 0 Render date: 2025-04-13T01:10:03.228Z Has data issue: false hasContentIssue false
  • English
  • Français

NOTE ON LEHMER–PIERCE SEQUENCES WITH THE SAME PRIME DIVISORS

Part of: Sequences and sets Elementary number theory

Published online by Cambridge University Press:  04 October 2017

M. SKAŁBA Open the ORCID record for M. SKAŁBA [Opens in a new window]
M. SKAŁBA*
Affiliation:
Institute of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 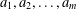$a_{1},a_{2},\ldots ,a_{m}$ and 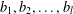$b_{1},b_{2},\ldots ,b_{l}$ be two sequences of pairwise distinct positive integers greater than 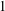$1$. Assume also that none of the above numbers is a perfect power. If for each positive integer $n$ and prime number 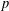$p$ the number 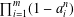$\prod _{i=1}^{m}(1-a_{i}^{n})$ is divisible by 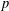$p$ if and only if the number 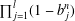$\prod _{j=1}^{l}(1-b_{j}^{n})$ is divisible by 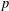$p$, then 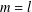$m=l$ and 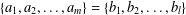$\{a_{1},a_{2},\ldots ,a_{m}\}=\{b_{1},b_{2},\ldots ,b_{l}\}$.

Keywords

Lehmer–Pierce sequencespower residues

MSC classification

Primary: 11B50: Sequences (mod $m$)
Secondary: 11A15: Power residues, reciprocity
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 11 - 14
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Barańczuk, S., ‘On a generalization of the support problem of Erdös and its analogues for abelian varieties and K-theory’, J. Pure Appl. Algebra 214 (2010), 380–384.CrossRefGoogle Scholar
Everest, G., van der Poorten, A., Shparlinski, I. and Ward, T., Recurrence Sequences, Mathematical Surveys and Monographs, 104 (American Mathematical Society, Providence, RI, 2003).CrossRefGoogle Scholar
Sanna, C., ‘Distribution of integral values for the ratio of two linear recurrences’, J. Number Theory 180 (2017), 195–207.CrossRefGoogle Scholar
Schinzel, A. and Skałba, M., ‘On power residues’, Acta Arith. 108 (2003), 77–94.CrossRefGoogle Scholar
Zannier, U., ‘Diophantine equations with linear recurrences. An overview of some recent progress’, J. Théor. Nombres Bordeaux 17(1) (2005), 423–435.CrossRefGoogle Scholar