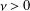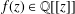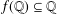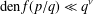Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
ÇALIŞKAN, Fatma
2019.
Lacunary Power Series and 𝑼𝒎-Numbers.
Celal Bayar Üniversitesi Fen Bilimleri Dergisi,
Vol. 15,
Issue. 4,
p.
365.
Lelis, Jean
and
Marques, Diego
2020.
On transcendental entire functions mapping Q into itself.
Journal of Number Theory,
Vol. 206,
Issue. ,
p.
310.
Lelis, Jean
Marques, Diego
Moreira, Carlos Gustavo
and
Trojovský, Pavel
2024.
A note on transcendental analytic functions with rational coefficients mapping $\mathbf{Q}$ into itself.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 100,
Issue. 8,