Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stojaković, Miloš
2001.
The Perimeter of optimal convex lattice polygons in the sense of different metrics.
Bulletin of the Australian Mathematical Society,
Vol. 63,
Issue. 2,
p.
229.
Stojaković, Miloš
2001.
On Finding The Limit Shape Of Optimal Convex Lattice Polygons.
Electronic Notes in Discrete Mathematics,
Vol. 10,
Issue. ,
p.
265.
Crombez, Loïc
Fonseca, Guilherme D. da
and
Gerard, Yan
2020.
Efficiently Testing Digital Convexity and Recognizing Digital Convex Polygons.
Journal of Mathematical Imaging and Vision,
Vol. 62,
Issue. 5,
p.
693.


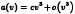 . We conjecture that
. We conjecture that 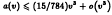 , and that for some positive constant
, and that for some positive constant 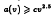 .
.