Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T17:33:34.405Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON ASYMPTOTIC NONBASES

Part of: Sequences and sets

Published online by Cambridge University Press:  13 October 2016

DENG-RONG LING
DENG-RONG LING*
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 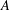$A$ be a subset of $\mathbb{N}$ , the set of all nonnegative integers. For an integer 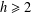$h\geq 2$ , let 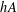$hA$ be the set of all sums of 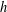$h$ elements of 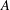$A$ . The set 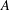$A$ is called an asymptotic basis of order 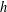$h$ if 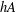$hA$ contains all sufficiently large integers. Otherwise, 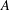$A$ is called an asymptotic nonbasis of order 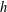$h$ . An asymptotic nonbasis 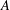$A$ of order 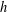$h$ is called a maximal asymptotic nonbasis of order 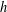$h$ if 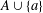$A\cup \{a\}$ is an asymptotic basis of order $h$ for every 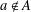$a\notin A$ . In this paper, we construct a sequence of asymptotic nonbases of order 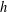$h$ for each 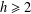$h\geq 2$ , each of which is not a subset of a maximal asymptotic nonbasis of order 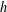$h$ .

Keywords

asymptotic nonbasismaximal asymptotic nonbasis

MSC classification

Primary: 11B13: Additive bases, including sumsets
Secondary: 11B34: Representation functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 1 , February 2017 , pp. 1 - 4
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Alladi, K. and Krantz, S., ‘Reflections on Paul Erdős on his birth centenary’, Notices Amer. Math. Soc. 62 (2015), 121–143.Google Scholar
Erdős, P. and Nathanson, M. B., ‘Maximal asymptotic nonbases’, Proc. Amer. Math. Soc. 48 (1975), 57–60.Google Scholar
Erdős, P. and Nathanson, M. B., ‘Oscillations of bases for the natural numbers’, Proc. Amer. Math. Soc. 53 (1975), 253–258.Google Scholar
Hennefeld, J., ‘Asymptotic nonbases which are not subsets of maximal asymptotic nonbases’, Proc. Amer. Math. Soc. 62 (1977), 23–24.Google Scholar
Nathanson, M. B., ‘Minimal bases and maximal nonbases in additive number theory’, J. Number Theory 6 (1974), 324–333.CrossRefGoogle Scholar