Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T01:48:33.942Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON ALMOST BALANCED BIPARTITIONS OF A GRAPH

Part of: Graph theory

Published online by Cambridge University Press:  14 October 2014

XIAOLAN HU ,
YUNQING ZHANG  and
YAOJUN CHEN
XIAOLAN HU
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, China
YUNQING ZHANG
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, China
YAOJUN CHEN*
Affiliation:
Department of Mathematics, Nanjing University, Nanjing 210093, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 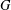$G$ be a graph of order 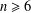$n\geq 6$ with minimum degree 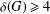${\it\delta}(G)\geq 4$. Arkin and Hassin [‘Graph partitions with minimum degree constraints’, Discrete Math. 190 (1998), 55–65] conjectured that there exists a bipartition 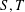$S,T$ of 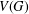$V(G)$ such that 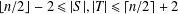$\lfloor n/2\rfloor -2\leq |S|,|T|\leq \lceil n/2\rceil +2$ and the minimum degrees in the subgraphs induced by 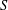$S$ and 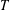$T$ are at least two. In this paper, we first show that 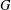$G$ has a bipartition such that the minimum degree in each part is at least two, and then prove that the conjecture is true if the complement of 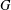$G$ contains no complete bipartite graph 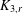$K_{3,r}$, where 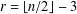$r=\lfloor n/2\rfloor -3$.

Keywords

almost balanced bipartitioncomplement

MSC classification

Primary: 05C70: Factorization, matching, partitioning, covering and packing
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 91 , Issue 2 , April 2015 , pp. 177 - 182
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Arkin, E. M. and Hassin, R., ‘Graph partitions with minimum degree constraints’, Discrete Math. 190 (1998), 55–65.Google Scholar
Diwan, A., ‘Decomposing graphs with girth at least five under degree constraints’, J. Graph Theory 33 (2000), 237–239.Google Scholar
El-Zahar, M., ‘On circuits in graphs’, Discrete Math. 50 (1984), 227–230.CrossRefGoogle Scholar
Kaneko, A., ‘On decomposition of triangle free graphs under degree constraints’, J. Graph Theory 27 (1998), 7–9.Google Scholar
Maurer, S. B., ‘Vertex colorings without isolates’, J. Combin. Theory Ser. B 27 (1979), 294–319.CrossRefGoogle Scholar
Stiebitz, M., ‘Decomposing graphs under degree constraints’, J. Graph Theory 23 (1996), 321–324.Google Scholar