Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-08T05:32:14.536Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on a paper of Bowcock and Yu

Published online by Cambridge University Press:  17 April 2009

I. P. Stavroulakis
I. P. Stavroulakis
Affiliation:
Department of MathematicsUniversity of Ioannina451 10 Ioanniana, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Consider the first order differential equation (1) 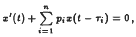, where pi, and τi, for i = 1,…,n, are positive constants. To find necessary and sufficient conditions, in terms of the coefficients and the delays only, under which all solutions of (1) oscillate, is a problem of great importence. In a recent paper, Bowcock and Yu claimed that 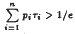is a necessary and sufficient condition for all solutions of (1) to be oscillatory. In this paper a counterexample shows that the above result is not valid and the error in this paper is indicated.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 40 , Issue 3 , December 1989 , pp. 421 - 424
Copyright
Copyright © Australian Mathematical Society 1989

References

[1]Arino, O., Györi, I. and Jawhari, A., ‘Oscillation criteria in delay equations’, J. Differential Equations 53 (1984), 115–123.CrossRefGoogle Scholar
[2]Bowcock, J.I. and Yu, Y.H., ‘Sharp conditions for oscillations caused by retarded and advanced perturbations’, Bull. Austral. Math. Soc. 37 (1988), 429–435.CrossRefGoogle Scholar
[3]Hunt, B.R. and Yorke, J.A., ‘When all solutions of oscillate’, J. Differential Equations 53 (1984), 139–145.Google Scholar
[4]Ladas, G., ‘Sharp conditions for oscillations caused by delays’, Appl. Anal. 9 (1979), 93–98.Google Scholar
[5]Ladas, C., Sficas, Y.G. and Stavroulakis, I.P., ‘Necessary and sufficient conditions for oscillations’, Amer. Math. Monthly 90 (1983), 637–640.Google Scholar
[6]Ladas, G. and Stavroulakis, I.P., ‘On delay differential inequalities of first order’, Funkcial. Ekvac. 25 (1982), 105–113.Google Scholar
[7]Ladas, G. and Stavroulakis, I.P., ‘Oscillations caused by several retarded and advanced arguments’, J. Differential Equations 44 (1982), 134–152.CrossRefGoogle Scholar
[8]Tramov, M.I., ‘Conditions for oscillatory solutions of first order differential equations with delayed arguments’, Izv. Vyssh. Uchebn. Zaved. Mat. 19 (1975), 92–96.Google Scholar