Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T13:22:04.987Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON A COMPLETE SOLUTION OF A PROBLEM POSED BY K. MAHLER

Part of: Entire and meromorphic functions, and related topics Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  03 May 2018

DIEGO MARQUES  and
CARLOS GUSTAVO MOREIRA
DIEGO MARQUES*
Affiliation:
Departamento de Matemática, Universidade de Brasília, Brasília, DF, Brazil email [email protected]
CARLOS GUSTAVO MOREIRA
Affiliation:
Instituto de Matemática Pura e Aplicada, Rio de Janeiro, RJ, Brazil email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 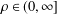$\unicode[STIX]{x1D70C}\in (0,\infty ]$ be a real number. In this short note, we extend a recent result of Marques and Ramirez [‘On exceptional sets: the solution of a problem posed by K. Mahler’, Bull. Aust. Math. Soc.94 (2016), 15–19] by proving that any subset of 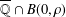$\overline{\mathbb{Q}}\cap B(0,\unicode[STIX]{x1D70C})$, which is closed under complex conjugation and contains 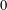$0$, is the exceptional set of uncountably many analytic transcendental functions with rational coefficients and radius of convergence 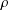$\unicode[STIX]{x1D70C}$. This solves the question posed by K. Mahler completely.

Keywords

Mahler problemtranscendental functionexceptional sets

MSC classification

Primary: 11J91: Transcendence theory of other special functions
Secondary: 30D35: Distribution of values, Nevanlinna theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 1 , August 2018 , pp. 60 - 63
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The authors were supported by CNPq-Brazil.

References

Mahler, K., ‘Arithmetic properties of lacunary power series with integral coefficients’, J. Aust. Math. Soc. 5 (1965), 56–64.CrossRefGoogle Scholar
Mahler, K., Lectures on Transcendental Numbers, Lecture Notes in Mathematics, 546 (Springer, Berlin, 1976).Google Scholar
Marques, D. and Ramirez, J., ‘On exceptional sets: the solution of a problem posed by K. Mahler’, Bull. Aust. Math. Soc. 94 (2016), 15–19.Google Scholar
Waldschmidt, M., ‘Algebraic values of analytic functions’, J. Comput. Appl. Math. 160 (2003), 323–333.CrossRefGoogle Scholar