Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-19T02:54:33.494Z Has data issue: false hasContentIssue false
  • English
  • Français

NORMAL SUBGROUPS WHOSE CONJUGACY CLASS GRAPH HAS DIAMETER THREE

Part of: Representation theory of groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  16 March 2016

ANTONIO BELTRÁN ,
MARÍA JOSÉ FELIPE  and
CARMEN MELCHOR
ANTONIO BELTRÁN*
Affiliation:
Departamento de Matemáticas, Universidad Jaume I, 12071 Castellón, Spain email [email protected]
MARÍA JOSÉ FELIPE
Affiliation:
Instituto Universitario de Matemática Pura y Aplicada, Universidad Politécnica de Valencia, 46022 Valencia, Spain email [email protected]
CARMEN MELCHOR
Affiliation:
Departamento de Educación, Universidad Jaume I, 12071 Castellón, Spain email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 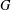$G$ be a finite group and let 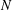$N$ be a normal subgroup of 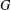$G$. We determine the structure of 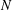$N$ when the diameter of the graph associated to the 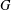$G$-conjugacy classes contained in 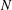$N$ is as large as possible, that is, equal to three.

Keywords

finite groupsconjugacy classesnormal subgroupsgraphs

MSC classification

Primary: 20D15: Nilpotent groups, $p$-groups
Secondary: 20E45: Conjugacy classes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 266 - 272
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Beltrán, A. and Felipe, M. J., ‘Prime powers as conjugacy class lengths of 𝜋-elements’, Bull. Aust. Math. Soc. 69 (2004), 317–325.Google Scholar
Beltrán, A., Felipe, M. J. and Melchor, C., ‘Graphs associated to conjugacy classes of normal subgroups in finite groups’, J. Algebra 443 (2015), 335–348.Google Scholar
Bertram, E. A., Herzog, M. and Mann, A., ‘On a graph related to conjugacy classes of groups’, Bull. Lond. Math. Soc. 22(6) (1990), 569–575.Google Scholar
Camina, A. R., ‘Arithmetical conditions on the conjugacy class numbers of a finite group’, J. Lond. Math. Soc. (2) 5 (1972), 127–132.Google Scholar
Casolo, C. and Dolfi, S., ‘The diameter of a conjugacy class graph of finite groups’, Bull. Lond. Math. Soc. 28 (1996), 141–148.Google Scholar
Dolfi, S., ‘Arithmetical conditions of the length of the conjugacy classes in finite groups’, J. Algebra 174(3) (1995), 753–771.CrossRefGoogle Scholar
The GAP Group, GAP – Groups, Algorithms, Programming, ver. 4.4.12 (2008).http://www.gap-system.org.Google Scholar
Kazarin, L. S., ‘On groups with isolated conjugacy classes’, Izv. Vyssh. Uchebn. Zaved. Mat. 1981(7) (1981), 40–45; For an English translation, see Soviet Mathematics 25(7) (1981), 43–49.Google Scholar