No CrossRef data available.
Article contents
NONRELATIVISTIC LIMIT FOR THE TRAVELLING WAVES OF THE PSEUDORELATIVISTIC HARTREE EQUATION
Published online by Cambridge University Press: 26 December 2024
Abstract
We consider the pseudorelativistic Hartree equation
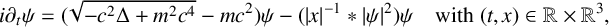 $$ \begin{align*} i\partial_t\psi=(\sqrt{-c^2\Delta +m^2c^4}-mc^2)\psi-(|x|^{-1}*|\psi|^2)\psi\quad \text{with } (t,x)\in\mathbb{R}\times\mathbb{R}^3, \end{align*} $$
$$ \begin{align*} i\partial_t\psi=(\sqrt{-c^2\Delta +m^2c^4}-mc^2)\psi-(|x|^{-1}*|\psi|^2)\psi\quad \text{with } (t,x)\in\mathbb{R}\times\mathbb{R}^3, \end{align*} $$which describes the dynamics of pseudorelativistic boson stars in the mean-field limit. We study the travelling waves of the form 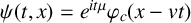 $\psi (t,x)=e^{it\mu }\varphi _{c}(x-vt)$, where
$\psi (t,x)=e^{it\mu }\varphi _{c}(x-vt)$, where 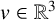 $v\in \mathbb {R}^3$ denotes the travelling velocity. We prove that
$v\in \mathbb {R}^3$ denotes the travelling velocity. We prove that  $\varphi _{c}$ converges strongly to the minimiser
$\varphi _{c}$ converges strongly to the minimiser 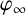 $\varphi _{\infty }$ of the limit energy
$\varphi _{\infty }$ of the limit energy 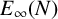 $E_{\infty }(N)$ in
$E_{\infty }(N)$ in 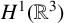 $H^1(\mathbb {R}^3)$ as the light speed
$H^1(\mathbb {R}^3)$ as the light speed  $c\to \infty $, where
$c\to \infty $, where 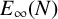 $E_{\infty }(N)$ is the corresponding energy for the limit equation
$E_{\infty }(N)$ is the corresponding energy for the limit equation
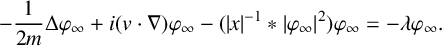 $$ \begin{align*} -\frac{1}{2m}\Delta\varphi_{\infty}+i(v\cdot\nabla)\varphi_{\infty}-({|x|^{-1}}*|\varphi_{\infty}|^2)\varphi_{\infty}=-\lambda\varphi_{\infty}. \end{align*} $$
$$ \begin{align*} -\frac{1}{2m}\Delta\varphi_{\infty}+i(v\cdot\nabla)\varphi_{\infty}-({|x|^{-1}}*|\varphi_{\infty}|^2)\varphi_{\infty}=-\lambda\varphi_{\infty}. \end{align*} $$Since the operator 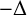 $-\Delta $ is the classical kinetic operator, we call this the nonrelativistic limit. We prove the existence of the minimiser for the limit energy
$-\Delta $ is the classical kinetic operator, we call this the nonrelativistic limit. We prove the existence of the minimiser for the limit energy  $E_{\infty }(N)$ by using concentration-compactness arguments.
$E_{\infty }(N)$ by using concentration-compactness arguments.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc
Footnotes
Q. Wang was partially supported by the National Natural Science Foundation of China (grant no. 11801519).



