Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tan, Kok-Keong
and
Xu, Hong Kun
1994.
Fixed point iteration processes for asymptotically nonexpansive mappings.
Proceedings of the American Mathematical Society,
Vol. 122,
Issue. 3,
p.
733.
Lin, Pei-Kee
Tan, Kok-Keong
and
Xu, Hong-Kun
1995.
Demiclosedness principle and asymptotic behavior for asymptotically nonexpansive mappings.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 24,
Issue. 6,
p.
929.
Tan, Kok-Keong
and
Xu, Hong-Kun
1996.
World Congress of Nonlinear Analysts '92.
p.
3025.
Oka, Hirokazu
1997.
An ergodic theorem for asymptotically nonexpansive mappings in the intermediate sense.
Proceedings of the American Mathematical Society,
Vol. 125,
Issue. 6,
p.
1693.
Kim, Jong Kyu
and
Li, Gang
2000.
Asymptotic behaviour for an almost-orbit of nonexpansive semigroups in Banach spaces.
Bulletin of the Australian Mathematical Society,
Vol. 61,
Issue. 2,
p.
345.
Xu, Hong-Kun
2001.
Strong asymptotic behavior of almost-orbits of nonlinear semigroups.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 46,
Issue. 1,
p.
135.
Luchuan, Zeng
2001.
Iterative approximation of fixed points of (asymptotically) nonexpansive mappings.
Applied Mathematics-A Journal of Chinese Universities,
Vol. 16,
Issue. 4,
p.
402.
Falset, Jesús Garcı́a
awa Kaczor, Wiesł
Kuczumow, Tadeusz
and
Reich, Simeon
2001.
Weak convergence theorems for asymptotically nonexpansive mappings and semigroups.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 43,
Issue. 3,
p.
377.
Rouhani, Behzad Djafari
and
Kim, Jong Kyu
2002.
Asymptotic behavior for almost-orbits of a reversible semigroup of non-Lipschitzian mappings in a metric space.
Journal of Mathematical Analysis and Applications,
Vol. 276,
Issue. 1,
p.
422.
Chidume, C.E.
2002.
Convergence theorems for asymptotically pseudocontractive mappings.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 49,
Issue. 1,
p.
1.
Kaczor, Wiesława
2002.
Weak convergence of almost orbits of asymptotically nonexpansive commutative semigroups.
Journal of Mathematical Analysis and Applications,
Vol. 272,
Issue. 2,
p.
565.
Chidume, C.E.
Ofoedu, E.U.
and
Zegeye, H.
2003.
Strong and weak convergence theorems for asymptotically nonexpansive mappings.
Journal of Mathematical Analysis and Applications,
Vol. 280,
Issue. 2,
p.
364.
Chidume, C. E.
Shahzad#, Naseer
and
Zegeye#, Habtu
2005.
Convergence Theorems for Mappings Which Are Asymptotically Nonexpansive in the Intermediate Sense.
Numerical Functional Analysis and Optimization,
Vol. 25,
Issue. 3-4,
p.
239.
Alber, YaI
Chidume, CE
and
Zegeye, H
2006.
Approximating fixed points of total asymptotically nonexpansive mappings.
Fixed Point Theory and Applications,
Vol. 2006,
Issue. 1,
Chidume, C.E.
and
Ali, Bashir
2007.
Approximation of common fixed points for finite families of nonself asymptotically nonexpansive mappings in Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 2,
p.
960.
Chidume, C.E.
and
Ofoedu, E.U.
2007.
Approximation of common fixed points for finite families of total asymptotically nonexpansive mappings.
Journal of Mathematical Analysis and Applications,
Vol. 333,
Issue. 1,
p.
128.
Chidume, C. E.
Ofoedu, E. U.
and
Popescu, Gelu
2009.
A New Iteration Process for Approximation of Common Fixed Points for Finite Families of Total Asymptotically Nonexpansive Mappings.
International Journal of Mathematics and Mathematical Sciences,
Vol. 2009,
Issue. 1,
Kozlowski, W.M.
2011.
Fixed point iteration processes for asymptotic pointwise nonexpansive mappings in Banach spaces.
Journal of Mathematical Analysis and Applications,
Vol. 377,
Issue. 1,
p.
43.
Dehaish, Buthinah A Bin
and
Kozlowski, WM
2012.
Fixed point iteration processes for asymptotic pointwise nonexpansive mapping in modular function spaces.
Fixed Point Theory and Applications,
Vol. 2012,
Issue. 1,
Kozlowski, W. M.
and
Sims, Brailey
2013.
Computational and Analytical Mathematics.
Vol. 50,
Issue. ,
p.
463.
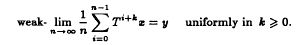
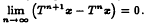 . We also present a weak convergence theorem for asymptotically nonexpansive semigroups.
. We also present a weak convergence theorem for asymptotically nonexpansive semigroups.