Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yamada, Mieko
1992.
Supplementary difference sets and Jacobi sums.
Discrete Mathematics,
Vol. 103,
Issue. 1,
p.
75.
Xia, Mingyuan
and
Liu, Gang
1995.
ON THE CLASS 1 *.
Acta Mathematica Scientia,
Vol. 15,
Issue. 4,
p.
361.
Xia, Mingyuan
1996.
SOME NEW FAMILIES OF SDSS AND HADAMARD MATRICES.
Acta Mathematica Scientia,
Vol. 16,
Issue. 2,
p.
153.
Xia, Ming-yuan
and
Liu, Gang
1996.
A new family of supplementary difference sets and Hadamard matrices.
Journal of Statistical Planning and Inference,
Vol. 51,
Issue. 3,
p.
283.
Martínez, Luis
Ðoković, Dragomir Z̆.
and
Vera‐López, Antonio
2004.
Existence question for difference families and construction of some new families.
Journal of Combinatorial Designs,
Vol. 12,
Issue. 4,
p.
256.


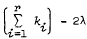 is the sum of
is the sum of 