No CrossRef data available.
Published online by Cambridge University Press: 06 October 2022
We characterise the existence of certain (weakly) compact multipliers of the second dual of symmetric abstract Segal algebras in both the group algebra 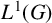 $L^{1}(G)$ and the Fourier algebra
$L^{1}(G)$ and the Fourier algebra 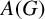 $A(G)$ of a locally compact group G.
$A(G)$ of a locally compact group G.
The research of the first author was in part supported by a grant from IPM (No. 1401170411).