Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-19T03:08:37.288Z Has data issue: false hasContentIssue false
  • English
  • Français

MORE ON THE ARENS REGULARITY OF 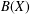$B(X)$

Part of: Topological algebras, normed rings and algebras, Banach algebras Linear spaces and algebras of operators

Published online by Cambridge University Press:  01 March 2016

R. FAAL  and
H. R. EBRAHIMI VISHKI
R. FAAL
Affiliation:
Department of Pure Mathematics, Ferdowsi University of Mashhad, PO Box 1159, Mashhad 91775, Iran email [email protected]
H. R. EBRAHIMI VISHKI*
Affiliation:
Department of Pure Mathematics and Center of Excellence in Analysis on Algebraic Structures (CEAAS), Ferdowsi University of Mashhad, PO Box 1159, Mashhad 91775, Iran email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We focus on a question raised by Daws [‘Arens regularity of the algebra of operators on a Banach space’, Bull. Lond. Math. Soc.36 (2004), 493–503] concerning the Arens regularity of 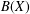$B(X)$, the algebra of operators on a Banach space 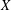$X$. Among other things, we show that 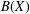$B(X)$ is Arens regular if and only if 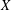$X$ is ultrareflexive.

Keywords

Arens productsalgebra of operatorsreflexive spacesuperreflexiveweak operator topologyultrapower

MSC classification

Primary: 47L10: Algebras of operators on Banach spaces and other topological linear spaces
Secondary: 46H25: Normed modules and Banach modules, topological modules (if not placed in or ) 47L50: Dual spaces of operator algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 296 - 303
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Arens, R., ‘The adjoint of a bilinear operation’, Proc. Amer. Math. Soc. 2 (1951), 839–848.CrossRefGoogle Scholar
Civin, P. and Yood, B., ‘The second conjugate space of a Banach algebra as an algebra’, Pacific J. Math. 11 (1961), 847–870.CrossRefGoogle Scholar
Dales, H. G., Banach Algebras and Automatic Continuity (Clarendon Press, Oxford, 2000).Google Scholar
Davis, W. J., Figiel, T., Johnson, W. B. and Pełczyński, A., ‘Factoring weakly compact operators’, J. Funct. Anal. 17 (1974), 311–327.CrossRefGoogle Scholar
Daws, M., ‘Arens regularity of the algebra of operators on a Banach space’, Bull. Lond. Math. Soc. 36 (2004), 493–503.CrossRefGoogle Scholar
Heinrich, S., ‘Ultraproducts in Banach space theory’, J. reine angew. Math. 313 (1980), 72–104.Google Scholar
Young, N. J., ‘Periodicity of functionals and representations of normed algebras on reflexive spaces’, Proc. Edinb. Math. Soc. (2) 20 (1976–77), 99–120.CrossRefGoogle Scholar