Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T20:39:00.620Z Has data issue: false hasContentIssue false
  • English
  • Français

MONOLITHIC BRAUER CHARACTERS

Part of: Representation theory of groups

Published online by Cambridge University Press:  28 March 2019

XIAOYOU CHEN  and
MARK L. LEWIS Open the ORCID record for MARK L. LEWIS [Opens in a new window]
XIAOYOU CHEN
Affiliation:
College of Science, Henan University of Technology, Zhengzhou 450001, China email [email protected]
MARK L. LEWIS*
Affiliation:
Department of Mathematical Sciences, Kent State University, Kent, OH 44242, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

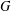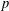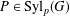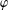Let $G$ be a group, $p$ be a prime and $P\in \text{Syl}_{p}(G)$. We say that a $p$-Brauer character $\unicode[STIX]{x1D711}$ is monolithic if 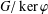$G/\ker \unicode[STIX]{x1D711}$ is a monolith. We prove that 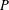$P$ is normal in 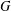$G$ if and only if 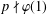$p\nmid \unicode[STIX]{x1D711}(1)$ for each monolithic Brauer character 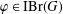$\unicode[STIX]{x1D711}\in \text{IBr}(G)$. When 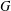$G$ is 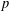$p$-solvable, we also prove that 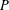$P$ is normal in 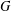$G$ and 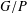$G/P$ is nilpotent if and only if 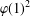$\unicode[STIX]{x1D711}(1)^{2}$ divides 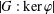$|G:\ker \unicode[STIX]{x1D711}|$ for all monolithic irreducible 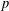$p$-Brauer characters 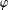$\unicode[STIX]{x1D711}$ of 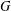$G$.

Keywords

Itô–Michler theoremmonolithic Brauer charactersSylow subgroup

MSC classification

Primary: 20C20: Modular representations and characters
Secondary: 20C15: Ordinary representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 434 - 439
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author is supported by the Fund for Young Key Teachers of Henan University of Technology, the Fund of Henan Administration of Foreign Experts Affairs, the Project of Henan Province (182102410049) and the NSFC (11571129 and 11771356).

References

Berkovich, Y. and Zhmud, E., ‘On monolithic characters’, Houston J. Math. 22 (1996), 263–278.Google Scholar
Chen, X., Cossey, J. P., Lewis, M. L. and Tong-Viet, H. P., ‘Blocks of small defect in alternating groups and squares of Brauer character degrees’, J. Group Theory 20 (2017), 1155–1173.Google Scholar
Chen, X. and Lewis, M. L., ‘Itô’s theorem and monomial Brauer characters’, Bull. Aust. Math. Soc. 96 (2017), 426–428.Google Scholar
Chen, X. and Lewis, M. L., ‘Squares of degrees of Brauer characters and monomial Brauer characters’, Bull. Aust. Math. Soc. to appear, doi:10.1017/S0004972718001442.Google Scholar
Gagola, S. M. Jr and Lewis, M. L., ‘A character theoretic condition characterizing nilpotent groups’, Comm. Algebra 27 (1999), 1053–1056.Google Scholar
Gallagher, P. X., ‘Group characters and normal Hall subgroups’, Nagoya Math. J. 21 (1962), 223–230.Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Isaacs, I. M., ‘Large orbits in actions of nilpotent groups’, Proc. Amer. Math. Soc. 127 (1999), 45–50.Google Scholar
Itô, N., ‘Some studies on group characters’, Nagoya Math. J. 2 (1951), 17–28.Google Scholar
Lu, J., ‘On a theorem of Gagola and Lewis’, J. Algebra Appl. 16 (2017), 1750158, 3 pp.Google Scholar
Lu, J., Qin, X. and Liu, X., ‘Generalizing a theorem of Gagola and Lewis characterizing nilpotent groups’, Arch. Math. 108 (2017), 337–339.Google Scholar
Michler, G. O., ‘Brauer’s conjectures and the classification of finite simple groups’, in: Representation Theory II. Groups and Orders, Lecture Notes in Mathematics, 1178 (Springer, Berlin, 1986), 129–142.Google Scholar
Navarro, G., Characters and Blocks of Finite Groups (Cambridge University Press, Cambridge, 1998).Google Scholar
Navarro, G., ‘Variations on the Itô–Michler theorem on character degrees’, Rocky Mountain J. Math. 46 (2016), 1363–1377.Google Scholar
Pang, L. and Lu, J., ‘Finite groups and degrees of irreducible monomial characters’, J. Algebra Appl. 15 (2016), 1650073, 4 pp.Google Scholar