No CrossRef data available.
Article contents
MONOGENIC EVEN QUARTIC TRINOMIALS
Published online by Cambridge University Press: 13 September 2024
Abstract
A monic polynomial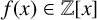 
$f(x)\in {\mathbb Z}[x]$ of degree N is called monogenic if 
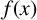$f(x)$ is irreducible over 
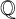${\mathbb Q}$ and 
$\{1,\theta ,\theta ^2,\ldots ,\theta ^{N-1}\}$ is a basis for the ring of integers of 
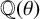${\mathbb Q}(\theta )$, where 
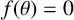$f(\theta )=0$. We prove that there exist exactly three distinct monogenic trinomials of the form 
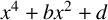$x^4+bx^2+d$ whose Galois group is the cyclic group of order 4. We also show that the situation is quite different when the Galois group is not cyclic.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
References
Cohen, H., A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics, 138 (Springer-Verlag, Berlin, 2000).Google Scholar
Harrington, J. and Jones, L., ‘Monogenic quartic polynomials and their Galois groups’, Preprint, 2024, arXiv:2404.05487v3.Google Scholar
Jakhar, A., Khanduja, S. and Sangwan, N., ‘Characterization of primes dividing the index of a trinomial’, Int. J. Number Theory 13(10) (2017), 2505–2514.CrossRefGoogle Scholar
Kappe, L.-C. and Warren, B., ‘An elementary test for the Galois group of a quartic polynomial’, Amer. Math. Monthly 96(2) (1989), 133–137.CrossRefGoogle Scholar
Swan, R., ‘Factorization of polynomials over finite fields’, Pacific J. Math. 12 (1962), 1099–1106.CrossRefGoogle Scholar