Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mushtaq, Q.
and
Aslam, M.
1993.
Group generated by two elements of orders 2 and 4 acting on real quadratic fields.
Acta Mathematica Sinica,
Vol. 9,
Issue. 1,
p.
48.
Mushtaq, Q.
and
Shaheen, F.
1994.
Factor groups of G6,6,6 through coset diagrams for an action on PL (Fq).
Discrete Mathematics,
Vol. 126,
Issue. 1-3,
p.
225.
Mushtaq, Qaiser
1998.
On word structure of the modular group over finite and real quadratic fields.
Discrete Mathematics,
Vol. 178,
Issue. 1-3,
p.
155.
Mushtaq, Q.
and
Aslam, M.
1998.
Group generated by two elements of orders two and six acting on R and Q(√n).
Discrete Mathematics,
Vol. 179,
Issue. 1-3,
p.
145.
Huu-Bong, Nguyen-
and
Mushtaq, Qaiser
2004.
Fibonacci and Lucas Numbers Through the Action of the Modular Group on Real Quadratic Fields.
The Fibonacci Quarterly,
Vol. 42,
Issue. 1,
p.
20.
Malik, M. Aslam
Husnine, S. M.
and
Majeed, Abdul
2005.
Properties of real quadratic irrational numbers under the action of the group H = áx, y: x2 = y4 = 1ñ.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 42,
Issue. 4,
p.
371.
Husnine, S. M.
Malik, M. Aslam
and
Majeed, Abdul
2005.
On ambiguous numbers of an invariant subset \documentclass{aastex} \usepackage{amsbsy} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{bm} \usepackage{mathrsfs} \usepackage{pifont} \usepackage{stmaryrd} \usepackage{textcomp} \usepackage{upgreek} \usepackage{portland,xspace} \usepackage{amsmath,amsxtra} \usepackage{bbm} \pagestyle{empty} \DeclareMathSizes{10}{9}{7}{6} \begin{document} \(Q^{*} \left(\sqrt {k^2m}\,\right)\) \end{document} of \documentclass{aastex} \usepackage{amsbsy} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{bm} \usepackage{mathrsfs} \usepackage{pifont} \usepackage{stmaryrd} \usepackage{textcomp} \usepackage{upgreek} \usepackage{portland,xspace} \usepackage{amsmath,amsxtra} \usepackage{bbm} \pagestyle{empty} \DeclareMathSizes{10}{9}{7}{6} \begin{document} \(Q\left(\sqrt m\,\right)\) \end{document} under the action of the modular group \documentclass{aastex} \usepackage{amsbsy} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{bm} \usepackage{mathrsfs} \usepackage{pifont} \usepackage{stmaryrd} \usepackage{textcomp} \usepackage{upgreek} \usepackage{portland,xspace} \usepackage{amsmath,amsxtra} \usepackage{bbm} \pagestyle{empty} \DeclareMathSizes{10}{9}{7}{6} \begin{document} \({\rm PSL}\, (2,Z)\) \end{document}.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 42,
Issue. 4,
p.
401.
Mushtaq, Q.
and
Hayat, U.
2007.
Pell Numbers, Pell–Lucas Numbers and Modular Group.
Algebra Colloquium,
Vol. 14,
Issue. 01,
p.
97.
Afzal, Farkhanda
Afzal, Qamar
and
Malik, M. Aslam
2013.
Quadratic Fields under the Action of Subgroups of M.
International Journal of Modeling and Optimization,
p.
283.
Malik, M. Aslam
and
Zafar, M. Asim
2014.
On Subsets of Q(&radic;<span style=" text-decoration:overline;">m</span>) Q under the Action of Hecke Groups H(&lambda;<sub>q</sub>).
Applied Mathematics,
Vol. 05,
Issue. 08,
p.
1284.
Mushtaq, Qaiser
and
Anis, Saima
2016.
Coset Diagram for the Action of Picard Group on $\mathbb{Q}(i,\sqrt{3})$.
Algebra Colloquium,
Vol. 23,
Issue. 01,
p.
33.
Razaq, Abdul
Mushtaq, Qaiser
and
Yousaf, Awais
2018.
The number of circuits of length 4 inPSL(2,ℤ)-space.
Communications in Algebra,
Vol. 46,
Issue. 12,
p.
5136.
Mushtaq, Qaiser
Razaq, Abdul
and
Yousaf, Awais
2019.
On contraction of vertices of the circuits in coset diagrams for
$${\varvec{PSL}}\varvec{(2}, \pmb {\mathbb {Z}} \varvec{)}$$
PSL
(
2
,
Z
)
.
Proceedings - Mathematical Sciences,
Vol. 129,
Issue. 1,
Rafiq, Ayesha
and
Khan, Majid
2019.
RETRACTED ARTICLE: Construction of new S-boxes based on triangle groups and its applications in copyright protection.
Multimedia Tools and Applications,
Vol. 78,
Issue. 11,
p.
15527.
Shahzad, Imran
Mushtaq, Qaiser
and
Razaq, Abdul
2019.
Construction of New S-Box Using Action of Quotient of the Modular Group for Multimedia Security.
Security and Communication Networks,
Vol. 2019,
Issue. ,
p.
1.
Rafiq, Ayesha
and
Mushtaq, Qaiser
2019.
Coset diagrams of the modular group and continued fractions.
Comptes Rendus. Mathématique,
Vol. 357,
Issue. 8,
p.
655.
Chen, Tianlan
Bari, Muhammad Nadeem
Malik, Muhammad Aslam
Afzal Siddiqui, Hafiz Muhammad
and
Liu, Jia-Bao
2020.
Icosahedral Group and Classification of PSL(2, Z)-Orbits of Real Quadratic Fields.
Journal of Mathematics,
Vol. 2020,
Issue. ,
p.
1.
Yousaf, Awais
Alolaiyan, Hanan
Razaq, Abdul
and
Younis, Muhammad
2020.
Evolution of ambiguous numbers under the actions of a Bianchi group.
Journal of Taibah University for Science,
Vol. 14,
Issue. 1,
p.
615.
Deajim, Abdulaziz
and
Hong, Shaofang
2021.
The Hecke Group
H
λ
4
Acting on Imaginary Quadratic Number Fields.
Journal of Mathematics,
Vol. 2021,
Issue. ,
p.
1.
Aamir, Muhammad
Awais Yousaf, Muhammad
Razaq, Abdul
and
Guardo, Elena
2021.
Number of Distinct Homomorphic Images in Coset Diagrams.
Journal of Mathematics,
Vol. 2021,
Issue. ,
p.
1.
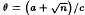 , where θ and its algebraic conjugate
, where θ and its algebraic conjugate 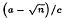 have different signs, and that part of the coset diagram containing such numbers forms a single circuit (closed path) and it is the only circuit in the orbit of θ.
have different signs, and that part of the coset diagram containing such numbers forms a single circuit (closed path) and it is the only circuit in the orbit of θ.

