Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Plagne, Alain
2002.
Maximal (k, l)-free sets in ℤ/pℤ are arithmetic progressions.
Bulletin of the Australian Mathematical Society,
Vol. 65,
Issue. 1,
p.
137.
Green, Ben
and
Ruzsa, Imre Z.
2005.
Sum-free sets in abelian groups.
Israel Journal of Mathematics,
Vol. 147,
Issue. 1,
p.
157.
Lev, Vsevolod F.
2005.
Large sum-free sets in ternary spaces.
Journal of Combinatorial Theory, Series A,
Vol. 111,
Issue. 2,
p.
337.
Lev, Vsevolod F.
2006.
Large sum-free sets in ℤ/ p ℤ.
Israel Journal of Mathematics,
Vol. 154,
Issue. 1,
p.
221.
SAMOTIJ, WOJCIECH
and
SUDAKOV, BENNY
2016.
The number of additive triples in subsets of abelian groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 160,
Issue. 3,
p.
495.
Hàn, Hiệp
and
Jiménez, Andrea
2018.
Maximum number of sum-free colorings in finite abelian groups.
Israel Journal of Mathematics,
Vol. 226,
Issue. 2,
p.
505.
Liu, Hong
and
Sharifzadeh, Maryam
2021.
Groups with few maximal sum-free sets.
Journal of Combinatorial Theory, Series A,
Vol. 177,
Issue. ,
p.
105333.
Balasubramanian, Ramachandran
Ramaré, Olivier
and
Srivastav, Priyamvad
2023.
Product of three primes in large arithmetic progressions.
International Journal of Number Theory,
Vol. 19,
Issue. 04,
p.
843.
Versteegen, Leo
2024.
The Structure of Large SUM-Free Sets in 𝔽n
p
.
The Quarterly Journal of Mathematics,
Vol. 75,
Issue. 3,
p.
1057.


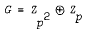 by Yap. We now prove this conjecture for groups
by Yap. We now prove this conjecture for groups 