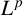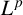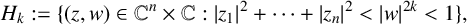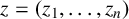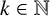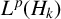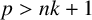$L^p$-BOUNDEDNESS OF THE BEREZIN TRANSFORM ON GENERALISED HARTOGS TRIANGLES

Abstract

We study the $L^p$-boundedness of the Berezin transform on the generalised Hartogs triangles which are defined by

$$ \begin{align*}H_k:=\{(z, w)\in\mathbb C^n\times\mathbb C: |z_1|^2+\cdots+|z_n|^2<|w|^{2k}<1\},\end{align*} $$

where $z=(z_1, \ldots , z_n)$ and $k\in \mathbb N$. We prove that the Berezin transform is bounded on $L^p(H_k)$ if and only if $p>nk+1$.

1. Introduction

The Berezin transform was introduced by Berezin in the 1970s, aiming to establish a quantisation procedure that associates a classical function on a symplectic manifold with a quantum operator on Hilbert space. It has been a very powerful tool in the field of complex analysis, functional analysis, differential geometry and quantum mechanics. Significant progress has been made on the study of Hankel operators, Toeplitz operators and Berezin–Toeplitz quantisation. For instance, Axler and Zheng [1] investigated the boundary behaviour of the Berezin transform to characterise the compactness of operators on the unit disk. Engli $\breve{\mathrm{s}}$ [8] generalised Axler and Zheng’s theorem to bounded symmetric domains. Zhu [17] also studied the Schatten norm of Hankel operators by using the Berezin transform. For related studies, see also [11, 16, 18, 19].

In this paper, we study the Berezin transform on a kind of generalised Hartogs triangle, which is defined by

(1.1) $$ \begin{align} H_k=\{(z, w)\in \mathbb C^n\times\mathbb C:|z_1|^2+\cdots+|z_n|^2<|w|^{2k}<1\}, \end{align} $$

where $z=(z_1, \ldots , z_n)$ and $k\in \mathbb N$ . When $k=n=1$ , this is the classical Hartogs triangle. By definition, the generalised Hartogs triangle is a bounded nonhomogeneous pseudoconvex domain with nonsmooth boundary. We will show that the Berezin transform is bounded on $L^p(H_k)$ if and only if $p>nk+1$ . As a direct corollary, the Berezin transform is unbounded on $L^p(H_k)$ if and only if $1\leq p\leq nk+1$ . To state our main results, we first introduce some notation.

Let $\Omega $ be a domain in $\mathbb {C}^n$ . Let $\mathcal {M}(\Omega )$ be the set of all complex measurable functions on $\Omega $ . For $p\geq 1$ , let $L^p(\Omega )$ be the standard $L^p$ -space with respect to the Lebesgue measure on $\mathbb {C}^n$ which is denoted by $dV$ . The norm on $L^p(\Omega )$ is given by

$$ \begin{align*} \Vert f\Vert_{p}=\bigg(\int_{\Omega} \vert f\vert^p\,dV(z)\bigg)^{1/p}. \end{align*} $$

Then $L^p(\Omega )$ becomes a Banach space under this norm. In particular, if $p=2$ , $L^2(\Omega )$ will be a Hilbert space, with the inner product

$$ \begin{align*} \langle f,g\rangle=\int_{\Omega}f(z)\overline{g(z)}\,dV(z) \end{align*} $$

and the $L^2$ -norm is denoted by $\|\cdot \|$ .

We denote by $\mathcal {O}(\Omega )$ the space of all holomorphic functions on $\Omega $ . We consider the Bergman space $A^2(\Omega )$ given by

$$ \begin{align*}A^2(\Omega):=\mathcal{O}(\Omega)\cap L^2(\Omega).\end{align*} $$

When $w\in \Omega $ , by Cauchy’s estimate,

$$ \begin{align*} \tau_{w}:A^2(\Omega)\rightarrow\mathbb{C},\quad f\mapsto \tau_{w}(f):=f(w) \end{align*} $$

is a bounded linear operator. By the Riesz representation theorem, we conclude that there exists a unique $K_{w}(\cdot ):=K(\cdot ,w)\in A^2(\Omega )$ such that

$$ \begin{align*} f(w)=\tau_{w}(f)=\langle f,K_w(\cdot)\rangle=\int_{\Omega}f(z)\overline{K(z,w)}\,dV(z). \end{align*} $$

We call $K:\Omega \times \Omega \rightarrow \mathbb {C}$ the Bergman kernel of $\Omega $ (or reproducing kernel of $A^{2}(\Omega )$ ).

The Bergman kernel $K(z, w)$ can be viewed as a Schwarz kernel of the orthogonal projection operator which we call the Bergman projection $P_{\Omega }:L^{2}(\Omega )\rightarrow A^2(\Omega ).$ Therefore,

$$ \begin{align*} P_{\Omega}f(z)=\int_{\Omega}f(w)K(z, w)\,dV(w). \end{align*} $$

In the following, assume that $K(z, z)\neq 0$ , for all $z\in \Omega $ . If $\Omega \subset \mathbb C^n$ is a bounded domain, it is easy to see that this assumption is always satisfied.

Definition 1.1. For any bounded linear operator $T: A^2(\Omega )\rightarrow A^2(\Omega )$ , we define the Berezin transform by

$$ \begin{align*} B_{\Omega}T(z)=\langle Tk_z,k_z\rangle,\;\;z\in \Omega, \end{align*} $$

where $k_z$ is the normalised Bergman kernel given by

$$ \begin{align*} k_z(w)=\frac{K(w,z)}{\sqrt{K(z,z)}}. \end{align*} $$

For any $h\in L^{\infty }(\Omega )$ , we associate h with the operator $T_h$ given by

$$ \begin{align*} T_h: A^2(\Omega)\rightarrow A^2(\Omega), \quad f\mapsto T_hf=P_{\Omega}(hf). \end{align*} $$

The operator $T_h$ is known as a Toeplitz operator and h is said to be the symbol of $T_h$ . Now we can define the Berezin transform of the function $h \in L^{\infty }(\Omega )$ by

(1.2) $$ \begin{align} B_{\Omega}h(z):=\frac{\langle hK(\cdot,z),K(\cdot,z)\rangle}{\langle K(\cdot,z),K(\cdot,z)\rangle}=\int_{\Omega}h(w)\frac{|K(w,z)|^2}{K(z, z)}\,dV(w). \end{align} $$

By the Cauchy–Schwarz inequality,

$$ \begin{align*} |\langle hK(\cdot, z),K(\cdot, z) \rangle|\leq\|hK(\cdot, z)\| \cdot\|K(\cdot, z)\|\leq\|h \|_{L^\infty(\Omega)}\|K(\cdot,z)\|^2. \end{align*} $$

It follows that the operator norm $\Vert B_{\Omega }\Vert \leq 1$ , regarding $B_\Omega $ as an operator from $L^\infty (\Omega )$ to itself, on any bounded domain $\Omega $ .

We consider the Hilbert space $L^2(H_k)$ on the generalised Hartogs triangle $H_k$ given by

$$ \begin{align*} L^2(H_{k}):=\bigg\{f \in \mathcal{M}(H_k):\int_{H_k}|f(Z)|^2 \,dV(Z)<\infty\bigg\}, \end{align*} $$

where $Z=(z_1,\ldots ,z_n,w)=(z,w)\in H_{k}$ .

As an important research object in complex analysis and complex geometry, the Hartogs triangles have been deeply studied from different perspectives and many important results have been obtained. For instance, Edholm and McNeal [7] and Chen [5] obtained the $L^p$ boundedness of the Bergman projection on the Hartogs triangles. Qin et al. [13] studied the $L^p$ -boundedness of Forelli–Rudin operators on the classical Hartogs triangle. In [4], Chakrabarit and Shaw investigated the Sobolev regularity of the $\overline {\partial }$ -equation on the Hartogs triangle. Bi and Hou [2] and Bi and Su [3] studied balanced metrics on the generalised Hartogs triangles.

We will focus our attention on the Berezin transform on the generalised Hartogs triangle $H_k$ . First, by (1.2), the Berezin transform of $L^\infty (H_{k})$ can be expressed as

$$ \begin{align*} B_{H_{k}}f(Z):=\int_{H_k}f(\widetilde{Z})\frac{|K_{H_k}(\widetilde{Z}, Z)|^2}{K_{H_k}(Z, Z)} \,dV(\widetilde{Z}), \end{align*} $$

where $K_{H_k}(Z, Z)$ is the Bergman kernel of $A^2(H_k)$ , $Z=(z, w)$ and $\widetilde Z=(\widetilde z, \widetilde w)$ . Moreover, since $H_k$ is biholomorphic on the product domain $\mathbb B^n\times D^\ast $ by the biholomorphic map

$$ \begin{align*}\varphi(z, w)=\bigg(\frac{z}{w^k}, w\bigg) \quad\text{for all } (z, w)\in H_k,\end{align*} $$

where ${z}/{w^k}:=({z_1}/{w^k}, \ldots , {z_n}/{w^k})$ , then by the transformation law of the Bergman kernel under biholomorphic maps, the Bergman kernel of $H_k$ is given by

$$ \begin{align*} K_{H_k}((z, w), (z, w))=\frac{|w|^{2k}}{(1-|w|^2)^2(|w|^{2k}-\|z\|^2)^{n+1}} =\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{-(n+1)}(1-|w|^2)^{-2}|w|^{-2nk}. \end{align*} $$

As far as we know, studies of the $L^p$ -regularity of the Berezin transform were mainly focused on homogeneous domains. Dostanić [6] obtained the $L^p$ regularity of the Berezin transform on the unit disk $\mathbb {D}$ and determined the explicit expression of the norm of the Berezin transform. Later, Marković [12] generalised Dostanić’s result to the unit ball in $\mathbb {C}^n$ . On the polydisk, Lee [10] established the interesting result that when $p>1$ , the Berezin transform is bounded on $L^p(\mathbb {D}^2)$ , while it is unbounded on $L^1(\mathbb {D}^2)$ . However, very little seems to be known about the regularity of the Berezin transform on nonhomogeneous domains. Recently, Gö $\check{\mathrm{g}}$ üş and Şahuto $\check{\mathrm{g}}$ lu [9] showed that the Berezin transform on $L^2(H)$ is unbounded where H is the classical Hartogs triangle given by $H=\{(z, w)\in \mathbb C^2: |z|<|w|<1\}$ . Thus, it is interesting to study the regularity of the Berezin transform on the generalised Hartogs triangles $H_k\subset \mathbb C^n\times \mathbb C$ when $n>1$ and $k>1$ . The main results of this paper are as follows.

Theorem 1.2. Let $H_k\subset \mathbb C^n\times \mathbb C$ be the generalised Hartogs triangle defined in (1.1). Then the Berezin transform $B_{H_k}$ on $L^p(H_{k})$ is bounded if and only if $p>nk+1$ .

As a direct corollary, we can also characterise the unboundedness of $B_{H_k}$ .

Corollary 1.3. For $p\geq 1$ , the Berezin transform $B_{H_{k}}$ on $L^p(H_{k})$ is unbounded if and only if $1\leq p\leq nk+1$ .

When $k=1$ and $n=1$ , the same result was obtained by Gö $\check{\mathrm{g}}$ üş and Şahuto $\check{\mathrm{g}}$ lu [9].

2. Preliminaries

First, we recall the following two crucial estimates from [13, 14].

Lemma 2.1. Suppose $c\in \mathbb R$ and $t>-1$ . Then the integral

$$ \begin{align*} J_{c, t}(z):=\int_{\mathbb B^n}\frac{(1-\|\xi\|^2)^t}{|1-\langle z, \xi\rangle|^{n+1+t+c}}\,dV(\xi), \quad z\in\mathbb B^n \end{align*} $$

has the following asymptotic properties:

1. (1) if $c<0$ , then $J_{c, t}$ is bounded on $\mathbb B^n$ ;

2. (2) if $c=0$ , then $J_{c, t}(z)\approx - \log {(1-\|z\|^2)}$ as $\|z\|\rightarrow 1$ ;

3. (3) if $c>0$ , then $J_{c, t}(z)\approx (1-\|z\|^2)^{-c}$ as $ \|z\|\rightarrow 1$ .

Lemma 2.2. Assume $\gamma \in \mathbb R, \alpha>-1$ and $\beta>-2$ . For $\eta \in D^\ast $ , the integral

$$ \begin{align*} J_{\alpha, \beta, \gamma}(\eta)=\int_{D^\ast}\frac{(1-|w|^2)^\alpha|w|^\beta}{|1-\eta\overline w|^\gamma}\,dV(w) \end{align*} $$

has the following asymptotic behaviour as $|\eta |\rightarrow 1$ :

1. (1) if $\alpha +2-\gamma>0$ , then $J_{\alpha , \beta , \gamma }(\eta )$ is bounded;

2. (2) if $\alpha +2-\gamma =0$ , then $J_{\alpha , \beta , \gamma }(z)\approx - \log {(1-|\eta |^2)}$ ;

3. (3) if $\alpha +2-\gamma <0$ , then $J_{\alpha , \beta , \gamma }(z)\approx (1-|\eta |^2)^{\alpha +2-\gamma }$ ;

4. (4) if $\alpha +2-\gamma <0$ and $-2<\beta \leq 0$ , then $J_{\alpha , \beta , \gamma }(\eta )\lesssim (1-|\eta |^2)^{\alpha +2-\gamma }|\eta |^\beta $ .

We also need the following two lemmas.

Lemma 2.3. For $a, b, c\in \mathbb R$ , define the integral

$$ \begin{align*} I_{a, b, c}:=\int_{H_k}\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^a(1-|w|^2)^b|w|^c \,dV(z, w). \end{align*} $$

Then $I_{a, b, c}<\infty $ if and only if $a>-1, ~b>-1, ~c>-2nk-2$ .

Proof. Since $\varphi : H_k\rightarrow \mathbb B^n\times D^\ast $ , $\varphi (z, w)=({z}/{w^k}, w)$ , is biholomorphic, by changing the coordinates $\xi ={z}/{w^k}, \eta =w$ , we obtain

$$ \begin{align*} I_{a, b, c}&=\int_{\mathbb B^n\times D^\ast}(1-\|\xi\|^2)^a(1-|\eta|^2)^b|\eta|^{c+2nk}\,dV(\xi, \eta) \notag\\ &=\int_{\mathbb B^n}(1-\|\xi\|^2)^adV(\xi)\cdot\int_{D^\ast}(1-|\eta|^2)^b|\eta|^{c+2nk}\,dV(\eta). \end{align*} $$

By using a polar coordinates transformation, it is easy to see that

$$ \begin{align*}\int_{\mathbb B^n}(1-\|\xi\|^2)^adV(\xi)<\infty\end{align*} $$

if and only if $a>-1$ . However,

$$ \begin{align*}\int_{D^\ast}(1-|\eta|^2)^b|\eta|^{c+2nk}dV(\eta)<\infty\end{align*} $$

if and only if

$$ \begin{align*}b>-1,\quad c+2nk>-2.\end{align*} $$

Thus, we get the conclusion of the lemma.

Lemma 2.4. Assume that $\gamma _1, \gamma _2\in \mathbb R$ , $\alpha _1, \alpha _2>-1$ and $\beta>-2nk-2$ . Denote

$$ \begin{align*} G(z, w)=\int_{H_k}\frac{(1-\|{x}/{y^k}\|^2)^{\alpha_1}}{|1-\langle{z}/{w^k}, {x}/{y^k}\rangle|^{\gamma_1}}\cdot \frac{(1-|y|^2)^{\alpha_2}|y|^\beta}{|1-w\overline y|^{\gamma_2}}\,dV(x, y), \quad (x, y)\in\mathbb C^n\times\mathbb C. \end{align*} $$

If $\alpha _1+n+1-\gamma _1<0$ and $\alpha _2+2-\gamma _2<0$ , then

$$ \begin{align*} G(z, w)\approx\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{\alpha_1+n+1-\gamma_1}(1-|w|^2)^{\alpha_2+2-\gamma_2} \end{align*} $$

as $|w|\rightarrow 1$ and $\|{z}/{w^k}\|\rightarrow 1$ .

Proof. Changing coordinates by $\xi ={x}/{y^k}, \eta =y$ , a direct calculation yields

$$ \begin{align*} G(z, w)&=\int_{H_k}\frac{(1-\|{x}/{y^k}\|^2)^{\alpha_1}}{|1-\langle{z}/{w^k}, {x}/{y^k}\rangle|^{\gamma_1}}\cdot \frac{(1-|y|^2)^{\alpha_2}|y|^\beta}{|1-w\overline y|^{\gamma_2}}\,dV(x, y) \notag\\ &=\int_{\mathbb B^n}\frac{(1-\|\xi\|^2)^{\alpha_1}}{|1-\langle{z}/{w^k}, \xi\rangle|^{\gamma_1}}\frac{(1-|\eta|^2)^{\alpha_2}}{|1-w\overline\eta|^{\gamma_2}}|\eta|^{\beta+2nk}\,dV(\xi, \eta) \notag \\ &=\int_{\mathbb B^n}\frac{(1-\|\xi\|^2)^{\alpha_1}}{|1-\langle{z}/{w^k}, \xi\rangle|^{\gamma_1}}dV(\xi)\cdot\int_{D^\ast}\frac{(1-|\eta|^2)^{\alpha_2}}{|1-w\overline\eta|^{\gamma_2}}\,dV(\eta). \end{align*} $$

By Lemmas 2.1 and 2.2, for $\alpha _1+n+1-\gamma _1<0$ and $\alpha _2+2-\gamma _2<0$ ,

$$ \begin{align*} \int_{\mathbb B^n}\frac{(1-\|\xi\|^2)^{\alpha_1}}{|1-\langle{z}/{w^k}, \xi\rangle|^{\gamma_1}}\,dV(\xi) & \approx \bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{\alpha_1+n+1-\gamma_1},\\ \int_{D^\ast}\frac{(1-|\eta|^2)^{\alpha_2}}{|1-w\overline\eta|^{\gamma_2}}|\eta|^{\beta+2nk}\,dV(\eta) & \approx(1-|w|^2)^{\alpha_2+2-\gamma_2}. \end{align*} $$

Thus, we get the conclusion of the lemma.

Assume $(X, \mu )$ is a measure space and $T(x, y)$ is a nonnegative measurable function on $X\times X$ . Let S be the integral operator induced by $T(x, y)$ , namely,

(2.1) $$ \begin{align} Sf(x)=\int_X T(x, y)f(y)\,d\mu(y). \end{align} $$

The following Schur’s test, from [15], is the most commonly used to investigate the boundedness of integral operators.

Theorem 2.5. Assume $1<p<\infty $ . Write $q={p}/{(p-1)}$ . The integral operator S defined as in (2.1) is bounded on $L^p(X, d\mu )$ if there exist a constant $C>0$ and a positive function h on X such that

$$ \begin{align*}\int_X T(x, y)h(y)^q\,d\mu(y)\leq Ch(x)^q \quad\text{for almost every } x\in X\end{align*} $$

and

$$ \begin{align*}\int_X T(x, y)h(x)^p\,d\mu(x)\leq Ch(y)^p \quad\text{for almost every } y\in X.\end{align*} $$

Moreover, $\|S\|\leq C$ .

Recall that

$$ \begin{align*} B_{H_k}f(z, w)&=\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{n+1}(1-|w|^2)^2|w|^{2nk}\\ &\quad \times\int_{H_k}\frac{1}{|w\overline\eta|^{2nk}|1-\langle{z}/{w^k}, {\xi}/{\eta^k} \rangle|^{2(n+1)}|1-w\overline\eta|^4}f(\xi, \eta)\,dV(\xi, \eta)\\ &=\int_{H_k}T((z, w), (x, y))f(x, y)\,dV(x, y), \end{align*} $$

where

$$ \begin{align*} T((z, w), (x, y))=\frac{(1-\|{z}/{w^k}\|^2)^{n+1}(1-|w|^2)^2|w|^{2nk}}{|w\overline y|^{2nk}|1-\langle {z}/{w^k}, {x}/{y^k}\rangle|^{2(n+1)}|1-w\overline y|^4}. \end{align*} $$

With the help of Schur’s test, we will prove the necessary and sufficient condition for the boundedness of $B_{H_k}$ in the next two sections.

3. Sufficiency for the boundedness of $B_{H_k}$

Lemma 3.1. If $p>nk+1$ , then $B_{H_k}$ is bounded on $L^p(H_k)$ .

Proof. Let $p'$ be the conjugate of p, that is, ${1}/{p}+{1}/{p'}=1$ . From $p>nk+1$ , the following intersections of intervals are nonempty:

(3.1) $$ \begin{align} \bigg(\!-\frac{1}{p'}, \frac{n+1}{p'}\bigg)\cap\bigg(-\frac{n+2}{p}, 0\bigg), \ \ \bigg(\!-\frac{3}{p}, 0\bigg)\cap\bigg(-\frac{1}{p'}, \frac{2}{p'}\bigg), \ \ \bigg(\frac{-2-2nk}{p}, \frac{-2nk}{p}\bigg]\cap\bigg(\frac{-2}{p'}, 0\bigg]. \end{align} $$

Now we use Schur’s test to show that $B_{H_k}$ is bounded on $L^p(H_k)$ . Let

$$ \begin{align*} h(z, w)=\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{\gamma_1}(1-|w|^2)^{\gamma_2}|w|^s, \end{align*} $$

where $\gamma _1, \gamma _2, s$ respectively lie in the three intervals in (3.1). It follows that

(3.2) $$ \begin{align} \left\{\, \begin{aligned} &\gamma_1p'>-1, \gamma_1p'-n-1<0\\ &\gamma_2p'>-1, \gamma_2p'-2<0\\ &\frac{-2}{p'}<s\leq0, \end{aligned} \right. \end{align} $$

and

(3.3) $$ \begin{align} \left\{\, \begin{aligned} &n+1+\gamma_1p>-1, ~~2+\gamma_2p>-1\\ &\gamma_1p<0, ~~\gamma_2p<0\\ &\frac{-2-2nk}{p}<s<\frac{-2nk}{p}. \end{aligned} \right. \end{align} $$

A straightforward calculation yields

$$ \begin{align*} &\int_{H_k} T((z, w), (\xi, \eta))h^{p'}(\xi, \eta)\,dV(\xi, \eta)\\ &\quad \lesssim \bigg(1-\!\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{n+1}(1-\!|w|^2)^2|w|^{2nk}\int_{H_k}\frac{(1-\|{x}/{y^k}\|^2)^{\gamma_1p'}(1-|y|^2)^{\gamma_2p'}|y|^{sp'}}{|w\overline y|^{2nk}|1-\!\langle {z}/{w^k}, {x}/{y^k}\rangle|^{2(n+1)}|1-w\overline y|^4}\,dV(x, y)\\ &\quad =\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{n+1}(1-|w|^2)^2 \\ &\qquad \times \int_{\mathbb B^n}\frac{(1-\|\xi\|^2)^{\gamma_1p'}}{|1-\langle{z}/{w^k}, \xi\rangle|^{2(n+1)}}\,dV(\xi) \int_{D^\ast}\frac{(1-|\eta|^2)^{\gamma_2p'}|\eta|^{sp'}}{|1-w\overline\eta|^4}\,dV(\eta). \end{align*} $$

By (3.2), and Lemmas 2.1 and 2.2,

(3.4) $$ \begin{align} &\int_{H_k} T((z, w), (\xi, \eta))h^{p'}(\xi, \eta)\,dV(\xi, \eta) \notag\\ &\quad \lesssim \bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{n+1}(1-|w|^2)^2\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{\gamma_1p'-n-1}(1-|w|^2)^{\gamma_2p'-2} \notag\\ &\quad =\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{\gamma_1p'}(1-|w|^2)^{\gamma_2p'} \lesssim h(z, w)^{p'}. \end{align} $$

Similarly,

$$ \begin{align*} \int_{H_k} & T((z, w), (x, y))h(z, w)^p\,dV(z, w)\\ &\lesssim|y|^{-2nk}\int_{H_k}\frac{(1-\|{z}/{w^k}\|^2)^{n+1+\gamma_1p}(1-|w|^2)^{2+\gamma_2p}|w|^{sp}}{|1-\langle{z}/{w^k}, {x}/{y^k}\rangle|^{2(n+1)}|1-w\overline y|^4}\,dV(z, w)\\ &=|y|^{-2nk}\int_{\mathbb B^n}\frac{(1-\|\xi\|^2)^{n+1+\gamma_1p}}{|1-\langle{x}/{y^k}, \xi\rangle|^{2(n+1)}}\,dV(\xi)\cdot\int_{D^\ast}\frac{(1-|w|^2)^{2+\gamma_2p}|w|^{2nk+sp}}{|1-w\overline\eta|^{4}}\,dV(\eta). \end{align*} $$

Then from (3.3), and Lemmas 2.1 and 2.2,

(3.5) $$ \begin{align} \int_{H_k}T((z, w), (x, y))h(z, w)^p\,dV(z, w)\lesssim|y|^{-2nk}\bigg(1-\bigg\|\frac{x}{y^k}\bigg\|^2\bigg)^{\gamma_1p}(1-|y|^2)^{\gamma_2p} \lesssim h(x, y)^p. \end{align} $$

From (3.4), (3.5) and Theorem 2.5, $B_{H_k}$ is bounded on $L^p(H_k)$ . This completes the proof of the lemma.

4. Necessity for the boundedness of $B_{H_k}$

To prove the necessity for the boundedness of $B_{H_k}$ , we first introduce a more general operator $S_{a, b, c}$ . For $a, b, c\in \mathbb R$ , we define

$$ \begin{align*} \begin{split} S_{a, b, c}f(z, w)&=\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{{(n+1)a}/{2}}(1-|w|^2)^a|w|^{ank}\\ &\quad \times\int_{H_k}\frac{(1-\|{\xi}/{\eta^k}\|^2)^{{(n+1)b}/{2}}(1-|\eta|^2)^b|\eta|^{bnk}}{(w\overline\eta)^{{cnk}/{2}}(1-\langle {z}/{w^k}, {\xi}/{\eta^k}\rangle)^{{(n+1)c}/{2}} (1-w\overline\eta)^c}f(\xi, \eta)\,dV(\xi, \eta). \end{split} \end{align*} $$

This is actually a kind of Forelli–Rudin operator defined on the generalised Hartogs triangle.

Proposition 4.1. Suppose $1<p<\infty $ and $a, b, c\in \mathbb R$ . If the operator $S=S_{a, b, c}$ is bounded on $L^p(H_k)$ , then

$$ \begin{align*} \left\{\, \begin{aligned} &-(n+1)ap<2, \quad - ap<1,\\ &(c-2a)nkp<4+4nk. \end{aligned} \right. \end{align*} $$

Proof. Set

$$ \begin{align*}K:=\bigg\{(\xi, \eta)\in H_k: \bigg(\frac{\xi}{\eta}, \eta\bigg)\in \mathbb B^n\times(D^\ast\setminus(-1, 0))\bigg\}\end{align*} $$

and

$$ \begin{align*}{ E}:=\bigg\{(\xi, \eta)\in H_k: \bigg\|\frac{\xi}{\eta}\bigg\|>\frac12, |\eta|>\frac12\bigg\}.\end{align*} $$

Consider the test function

$$ \begin{align*} f_{M, c}(\xi, \eta)=\begin{cases} {\chi_E}(\xi, \eta)\overline \eta^{{cnk}/{2}}\bigg[|\eta|\bigg(1-\bigg\|\dfrac{\xi}{\eta}\bigg\|^2\bigg)(1-|\eta|^2)\bigg]^M & \text{for } (\xi, \eta)\in K\\ 0 & \text{for } (\xi, \eta)\in H_k\setminus K, \end{cases} \end{align*} $$

where $\chi _E$ is the characteristic function of the set E and M is a nonnegative real number such that $M+{(n+1)b}/{2}>-1$ . Then, from the assumption,

$$ \begin{align*} \|f_{M, c}\|^p_{L^p}=\int_E|\eta|^{{cnkp}/{2}+pM}(1-|\eta|^2)^{pM}\bigg(1-\bigg\|\frac{\xi}{\eta^k}\bigg\|\bigg)^{pM}\,dV(\xi, \eta)<\infty. \end{align*} $$

Thus, $f_{M, c}\in L^p(H_k)$ . Set $\mathbb B^n(\tfrac 12):=\{z\in \mathbb B^n: \|z\|>\frac 12\}$ . Then,

$$ \begin{align*} S_{a, b, c}f_{M, c}&=K_{H_k}((z, w), (z, w))^{-{a}/{2}}w^{-{cnk}/{2}} \\ &\quad\times \int_{E}\frac{(1-\|{\xi}/{\eta^k}\|^2)^{{(n+1)b}/{2}+M}(1-|\eta|^2)^{b+M}|\eta|^{bnk+M}}{(1-\langle {z}/{w^k}, {\xi}/{\eta^k}\rangle)^{{(n+1)c}/{2}}(1-w\overline\eta)^c}\,dV(\xi, \eta)\\ &=K_{H_k}((z, w), (z, w))^{-{a}/{2}}w^{-{cnk}/{2}}\int_{\mathbb B^n(\frac12)}\frac{(1-\|\xi\|^2)^{{(n+1)b}/{2}+M}}{(1-\langle {z}/{w^k}, \xi\rangle)^{{(n+1)c}/{2}}}\,dV(\xi)\\ &\quad\times \int_{\mathbb B^1(\frac12)}\frac{(1-|\eta|^2)^{M+b}|\eta|^{bnk+M+2nk}}{(1-w\overline\eta)^c}\,dV(\eta)\\ &=C_MK_{H_k}((z, w), (z, w))^{-{a}/{2}}w^{-{cnk}/{2}}, \end{align*} $$

where $C_M$ is a constant. The last equality follows from the assumption that $M\geq 0$ and $M+{(n+1)b}/{2}>-1$ . The boundedness assumption for $S_{a, b, c}$ on $L^p(H_k) $ implies that $S_{a, b, c}f_{M, c}\in L^p(H_k)$ . Thus,

$$ \begin{align*} \int_{H_k} K_{H_k}((z, w), (z, w))^{-{a}/{2}p}|w|^{-{cnk}/{2}p}\,dV(z, w)<\infty. \end{align*} $$

That is,

$$ \begin{align*} \int_{H_k}\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{{(n+1)ap}/{2}}(1-|w|^2)^{ap}|w|^{ankp-{cnkp}/{2}}\,dV(z, w)<\infty. \end{align*} $$

Finally, by Lemma 2.3, $-(n+1)ap<2, \,ap<1$ and $(c-2a)nkp<4+4nk$ .

A duality argument gives the next proposition.

Proposition 4.2. Suppose $1<p<\infty $ and $a, b, c\in \mathbb R$ . If the operator $S_{a, b, c}$ is bounded on $L^p(H_k)$ , then

$$ \begin{align*} \left\{\, \begin{aligned} &2<[(n+1)b+2]p,~~1<(b+1)p,\\ &4+4nk<[(2b-c)nk+4nk+4]p. \end{aligned} \right. \end{align*} $$

Proof. Let q be the conjugate of p and $S^\ast _{a, b, c}: L^q(H_k)\rightarrow L^q(H_k)$ be the adjoint operator of $S_{a, b, c}$ . By the assumption, $S^\ast _{a, b, c}$ is also bounded on $L^q(H_k)$ . A direct calculation shows that

$$ \begin{align*} S^\ast_{a, b, c}f(z, w)&=\bigg(1-\bigg\|\frac{z}{w^k}\bigg\|^2\bigg)^{{(n+1)b}/{2}}(1-|w|^2)^{b}|w|^{bnk}\\ &\quad\times \int_{H_k}\frac{(1-\|{\xi}/{\eta^k}\|^2)^{{(n+1)a}/{2}}(1-|\eta|^2)^{a}|\eta|^{ank}}{(w\overline\eta)^{{cnk}/{2}}(1-\langle {z}/{w^k}, {\xi}/{\eta^k}\rangle)^{{(n+1)c/}{2}}(1-w\overline\eta)^c}f(\xi, \eta)\,dV(\xi, \eta). \end{align*} $$

Since $S^\ast _{a, b, c}$ is bounded on $L^q(H_k)$ , then by Lemma 4.1,

$$ \begin{align*} \left\{\, \begin{aligned} &-(n+1)bq<2, \quad -bq<1\\ &(c-2b)nkq<4+4nk. \end{aligned} \right. \end{align*} $$

Substituting $q={p}/{(p-1)}$ yields the conclusion of the proposition.

The next lemma is a direct corollary of Proposition 4.2.

Lemma 4.3. Suppose $1<p<\infty $ . If the Berezin transform $B_{H_k}$ is bounded on $L^p(H_k)$ , then $p>nk+1$ .

Proof. Choose $a=2, b=0, c=4$ . Since $S_{2, 0, 4}=B_{H_k}$ , the conclusion of this lemma follows from Proposition 4.2.

Lemmas 3.1 and 4.3 establish our main result, Theorem 1.2.