Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T16:42:35.630Z Has data issue: false hasContentIssue false
  • English
  • Français

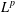$L^{p}$-APPROXIMATION OF HOLOMORPHIC FUNCTIONS ON A CLASS OF CONVEX DOMAINS

Part of: Differential operators in several variables Pseudoconvex domains Approximations and expansions Holomorphic convexity

Published online by Cambridge University Press:  23 April 2018

LY KIM HA Open the ORCID record for LY KIM HA [Opens in a new window]
LY KIM HA*
Affiliation:
Faculty of Mathematics and Computer Science, University of Science, Vietnam National University, HoChiMinh City (VNU-HCM), 227 Nguyen Van Cu street, District 5, Ho Chi Minh City, Vietnam email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 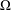$\unicode[STIX]{x1D6FA}$ be a member of a certain class of convex ellipsoids of finite/infinite type in 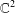$\mathbb{C}^{2}$. In this paper, we prove that every holomorphic function in 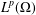$L^{p}(\unicode[STIX]{x1D6FA})$ can be approximated by holomorphic functions on 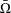$\bar{\unicode[STIX]{x1D6FA}}$ in 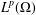$L^{p}(\unicode[STIX]{x1D6FA})$-norm, for 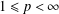$1\leq p<\infty$. For the case 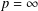$p=\infty$, the continuity up to the boundary is additionally required. The proof is based on 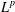$L^{p}$ bounds in the additive Cousin problem.

Keywords

Lp approximationholomorphic functionsHenkin solutionsthe additive Cousin problemfinite/infinite type

MSC classification

Primary: 32E30: Holomorphic and polynomial approximation, Runge pairs, interpolation
Secondary: 32T25: Finite type domains 32W05: $overlinepartial$ and $overlinepartial$-Neumann operators 41A63: Multidimensional problems (should also be assigned at least one other classification number in this section) 41A65: Abstract approximation theory (approximation in normed linear spaces and other abstract spaces)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 446 - 452
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Bedford, E. and Fornaess, J. E., ‘A construction of peak functions on weakly pseudoconvex domains’, Ann. of Math. (2) 107 (1978), 555–568.CrossRefGoogle Scholar
Beatrous, F. and Range, R. M., ‘On holomorphic approximation in weakly pseudoconvex domains’, Pacific J. Math. 89(2) (1980), 249–255.Google Scholar
Cole, B. and Range, R. M., ‘A-measures on complex manifolds and some applications’, J. Funct. Anal. 11 (1972), 394–400.CrossRefGoogle Scholar
Diederich, K. and Fornaess, J. E., ‘Pseudoconvex domains: an example with nontrivial Nebenhülle’, Math. Ann. 225 (1977), 275–292.CrossRefGoogle Scholar
Davie, A. M., Gamelin, T. W. and Garnett, J., ‘Distance estimates and pointwise bounded density’, Trans. Amer. Math. Soc. 175 (1973), 37–68.Google Scholar
Grauert, H. and Lieb, I., ‘Das Ramirezsche Integral und die Lösung der Gleichung ∂̄f =𝛼 im Bereich der beschränkten Formen’, in: Proc. Conf. Complex Analysis, Rice University, 1969, Rice University Studies, 56 (1970), 29–50.Google Scholar
Henkin, G. M., ‘Integral representations of functions holomorphic in strictly-pseudoconvex domains and some applications’, Math. USSR Sbornik. 7(4) (1969), 597–616.CrossRefGoogle Scholar
Ha, L. K., Khanh, T. V. and Raich, A., ‘ L p -estimates for the ∂̄-equation on a class of infinite type domains’, Int. J. Math. 25 (2014), Article ID 1450106, 15 pages.CrossRefGoogle Scholar
Kerzman, N., ‘Hölder and L p estimates for solutions of ∂̄u = f in strongly pseudoconvex domains’, Comm. Pure Appl. Math. 24 (1971), 301–379.Google Scholar
Kohn, J. J. and Nirenberg, L., ‘A pseudo-convex domain not admitting a holomorphic support function’, Math. Ann. 201 (1973), 265–268.Google Scholar
Lieb, I., ‘Ein approximationssatz auf streng pseudokonvexen Gebieten’, Math. Ann. 184 (1969), 56–60.Google Scholar
Range, R. M., Holomorphic Functions and Integral Representations in Several Complex Variables (Springer, Berlin–New York, 1986).CrossRefGoogle Scholar
Rudin, W., Real and Complex Analysis (McGraw-Hill, New York, 1966).Google Scholar