Hostname: page-component-6bf8c574d5-86b6f Total loading time: 0 Render date: 2025-03-07T11:59:56.107Z Has data issue: false hasContentIssue false
  • English
  • Français

LOGARITHMIC COEFFICIENTS OF SOME CLOSE-TO-CONVEX FUNCTIONS

Part of: Geometric function theory

Published online by Cambridge University Press:  02 November 2016

MD FIROZ ALI  and
A. VASUDEVARAO
MD FIROZ ALI
Affiliation:
Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur-721 302, West Bengal, India email [email protected]
A. VASUDEVARAO*
Affiliation:
Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur-721 302, West Bengal, India email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The logarithmic coefficients 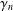$\unicode[STIX]{x1D6FE}_{n}$ of an analytic and univalent function 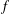$f$ in the unit disc 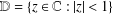$\mathbb{D}=\{z\in \mathbb{C}:|z|<1\}$ with the normalisation 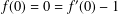$f(0)=0=f^{\prime }(0)-1$ are defined by 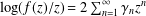$\log (f(z)/z)=2\sum _{n=1}^{\infty }\unicode[STIX]{x1D6FE}_{n}z^{n}$. In the present paper, we consider close-to-convex functions (with argument 0) with respect to odd starlike functions and determine the sharp upper bound of 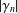$|\unicode[STIX]{x1D6FE}_{n}|$, 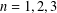$n=1,2,3$, for such functions 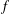$f$.

Keywords

analyticunivalentstarlikeconvexclose-to-convex functionslogarithmic coefficient

MSC classification

Primary: 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Secondary: 30C55: General theory of univalent and multivalent functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 95 , Issue 2 , April 2017 , pp. 228 - 237
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by the University Grants Commission through a UGC-SRF Fellowship. The second author was supported by SERB (DST).

References

Ali, Md F. and Vasudevarao, A., ‘On logarithmic coefficients of some close-to-convex functions’, Preprint, 2016, arXiv:1606.05162.CrossRefGoogle Scholar
Bazilevich, I. E., ‘Coefficient dispersion of univalent functions’, Mat. Sb. 68(110) (1965), 549–560.Google Scholar
Bazilevich, I. E., ‘On a univalence criterion for regular functions and the dispersion of their derivatives’, Mat. Sb. 74(116) (1967), 133–146.Google Scholar
de Branges, L., ‘A proof of the Bieberbach conjecture’, Acta Math. 154(1–2) (1985), 137–152.CrossRefGoogle Scholar
Duren, P. L., Univalent Functions, Grundlehren der mathematischen Wissenschaften, 259 (Springer, New York, Berlin, Heidelberg, Tokyo, 1983).Google Scholar
Duren, P. L. and Leung, Y. J., ‘Logarithmic coefficients of univalent functions’, J. Anal. Math. 36 (1979), 36–43.Google Scholar
Elhosh, M. M., ‘On the logarithmic coefficients of close-to-convex functions’, J. Aust. Math. Soc. Ser. A 60 (1996), 1–6.Google Scholar
Girela, D., ‘Logarithmic coefficients of univalent functions’, Ann. Acad. Sci. Fenn. Math. 25 (2000), 337–350.Google Scholar
Goodman, A. W., Univalent Functions, Vols. I and II (Mariner, Tampa, FL, 1983).Google Scholar
Hayman, W. K., Multivalent Functions (Cambridge University Press, Cambridge, 1958).Google Scholar
Libera, R. J. and Złotkiewicz, E. J., ‘Early coefficients of the inverse of a regular convex function’, Proc. Amer. Math. Soc. 85(2) (1982), 225–230.Google Scholar
Ma, W. and Minda, D., ‘A unified treatment of some special classes of univalent functions’, in: Proceedings of the Conference on Complex Analysis (Tianjin, 1992) (eds. Li, Z., Ren, F., Lang, L. and Zhang, S.) (International Press, Cambridge, MA, 1994), 157–169.Google Scholar
Pranav Kumar, U. and Vasudevarao, A., ‘Logarithmic coefficients for certain subclasses of close-to-convex functions’, Preprint, 2016, arXiv:1607.01843v2.Google Scholar
Roth, O., ‘A sharp inequality for the logarithmic coefficients of univalent functions’, Proc. Amer. Math. Soc. 135(7) (2007), 2051–2054.Google Scholar
Thomas, D. K., ‘On the logarithmic coefficients of close to convex functions’, Proc. Amer. Math. Soc. 144 (2016), 1681–1687.Google Scholar