Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-12T03:46:21.974Z Has data issue: false hasContentIssue false
  • English
  • Français

THE LOCAL 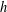$h$-POLYNOMIALS OF CLUSTER SUBDIVISIONS HAVE ONLY REAL ZEROS

Part of: Polynomials, rational functions Algebraic combinatorics Combinatorics Polytopes and polyhedra

Published online by Cambridge University Press:  01 August 2018

PHILIP B. ZHANG Open the ORCID record for PHILIP B. ZHANG [Opens in a new window]
PHILIP B. ZHANG*
Affiliation:
College of Mathematical Science, Tianjin Normal University, Tianjin 300387, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Athanasiadis [‘A survey of subdivisions and local 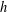$h$-vectors’, in The Mathematical Legacy of Richard P. Stanley (American Mathematical Society, Providence, RI, 2017), 39–51] asked whether the local 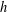$h$-polynomials of type 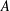$A$ cluster subdivisions have only real zeros. We confirm this conjecture and prove that the local 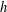$h$-polynomials for all the Cartan–Killing types have only real roots. Our proofs use multiplier sequences and Chebyshev polynomials of the second kind.

Keywords

real-rootednessmultiplier sequencelocal h-polynomialcluster subdivisionChebyshev polynomial of the second kind

MSC classification

Primary: 26C10: Polynomials
Secondary: 05A15: Exact enumeration problems, generating functions 05E45: Combinatorial aspects of simplicial complexes 52B45: Dissections and valuations (Hilbert's third problem, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 98 , Issue 2 , October 2018 , pp. 258 - 264
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the National Science Foundation of China (Nos. 11626172 and 11701424), the TJNU Funding for Scholars Studying Abroad, the PhD Program of TJNU (No. XB1616) and MECF of Tianjin (No. JW1713).

References

Athanasiadis, C. A., ‘A survey of subdivisions and local h-vectors’, in: The Mathematical Legacy of Richard P. Stanley (American Mathematical Society, Providence, RI, 2017), 39–51.Google Scholar
Athanasiadis, C. A. and Savvidou, C., ‘The local h-vector of the cluster subdivision of a simplex’, Sém. Lothar. Combin. 66 (2011–2012), Article ID B66c, 21 pages.Google Scholar
Brändén, P., ‘Iterated sequences and the geometry of zeros’, J. reine angew. Math. 658 (2011), 115–131.Google Scholar
Craven, T. and Csordas, G., ‘Problems and theorems in the theory of multiplier sequences’, Serdica Math. J. 22 (1996), 515–524.Google Scholar
Craven, T. and Csordas, G., ‘Composition theorems, multiplier sequences and complex zero decreasing sequences’, in: Value Distribution Theory and Related Topics, Advances in Complex Analysis and its Applications, 3 (Kluwer Academic, Boston, MA, 2004), 131–166.Google Scholar
Fomin, S. and Zelevinsky, A., ‘Cluster algebras. I. Foundations’, J. Amer. Math. Soc. 15 (2002), 497–529.Google Scholar
Fomin, S. and Zelevinsky, A., ‘ Y-systems and generalized associahedra’, Ann. of Math. (2) 158 (2003), 977–1018.Google Scholar
Liu, L. L. and Wang, Y., ‘A unified approach to polynomial sequences with only real zeros’, Adv. Appl. Math. 38 (2007), 542–560.Google Scholar
Petersen, T. K., Eulerian Numbers, Birkhäuser Advanced Texts: Basel Textbooks (Birkhäuser/Springer, New York, 2015).Google Scholar
Pólya, G. and Schur, J., ‘Über zwei Arten von Faktorenfolgen in der Theorie der algebraischen Gleichungen’, J. reine angew. Math. 144 (1914), 89–113.Google Scholar
Rahman, Q. I. and Schmeisser, G., Analytic Theory of Polynomials, London Mathematical Society Monographs: New Series, 26 (The Clarendon Press/Oxford University Press, Oxford, 2002).Google Scholar
Stanley, R. P., ‘Subdivisions and local h-vectors’, J. Amer. Math. Soc. 5 (1992), 805–851.Google Scholar