Hostname: page-component-f554764f5-nqxm9 Total loading time: 0 Render date: 2025-04-18T10:59:37.071Z Has data issue: false hasContentIssue false
  • English
  • Français

LIPSCHITZ RETRACTION OF FINITE SUBSETS OF HILBERT SPACES

Part of: Basic constructions Maps and general types of spaces defined by maps Spaces with richer structures

Published online by Cambridge University Press:  08 July 2015

LEONID V. KOVALEV
LEONID V. KOVALEV*
Affiliation:
215 Carnegie, Mathematics Department, Syracuse University, Syracuse, NY 13244-1150, USA email lvkovale@syr.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Finite subset spaces of a metric space 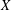$X$ form a nested sequence under natural isometric embeddings 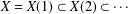$X=X(1)\subset X(2)\subset \cdots \,$. We prove that this sequence admits Lipschitz retractions 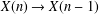$X(n)\rightarrow X(n-1)$ when 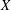$X$ is a Hilbert space.

Keywords

finite subset spaceHausdorff metricLipschitz retractionmetric space

MSC classification

Primary: 54E40: Special maps on metric spaces
Secondary: 54B20: Hyperspaces 54C15: Retraction 54C25: Embedding
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 93 , Issue 1 , February 2016 , pp. 146 - 151
Copyright
© 2015 Australian Mathematical Publishing Association Inc. 

References

Borsuk, K. and Ulam, S., ‘On symmetric products of topological spaces’, Bull. Amer. Math. Soc. 37(12) (1931), 875–882.CrossRefGoogle Scholar
Bridson, M. R. and Haefliger, A., Metric Spaces of Non-positive Curvature, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 319 (Springer, Berlin, 1999).CrossRefGoogle Scholar
Capogna, L., Tyson, J. and Wenger, S. (ed..s.), AimPL: Mapping Theory in Metric Spaces (American Institute of Mathematics, Palo Alto, 2012), available from http://aimpl.org/mappingmetric.Google Scholar
Goblet, J., ‘Lipschitz extension of multiple Banach-valued functions in the sense of Almgren’, Houston J. Math. 35(1) (2009), 223–231.Google Scholar
Kovalev, L. V., ‘Symmetric products of the line: embeddings and retractions’, Proc. Amer. Math. Soc. 143(2) (2015), 801–809.CrossRefGoogle Scholar
Mostovoy, J., ‘Lattices in ℂ and finite subsets of a circle’, Amer. Math. Monthly 111(4) (2004), 357–360.Google Scholar
Rockafellar, R. T., Convex Analysis, Princeton Landmarks in Mathematics (Princeton University Press, Princeton, NJ, 1997).Google Scholar
Tuffley, C., ‘Finite subset spaces of S 1’, Algebr. Geom. Topol. 2 (2002), 1119–1145.CrossRefGoogle Scholar