Article contents
LINEAR INDEPENDENCE OF POWERS OF SINGULAR MODULI OF DEGREE THREE
Published online by Cambridge University Press: 12 September 2018
Abstract
We show that two distinct singular moduli 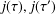 $j(\unicode[STIX]{x1D70F}),j(\unicode[STIX]{x1D70F}^{\prime })$, such that for some positive integers
$j(\unicode[STIX]{x1D70F}),j(\unicode[STIX]{x1D70F}^{\prime })$, such that for some positive integers 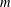 $m$ and
$m$ and  $n$ the numbers
$n$ the numbers 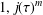 $1,j(\unicode[STIX]{x1D70F})^{m}$ and
$1,j(\unicode[STIX]{x1D70F})^{m}$ and 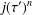 $j(\unicode[STIX]{x1D70F}^{\prime })^{n}$ are linearly dependent over
$j(\unicode[STIX]{x1D70F}^{\prime })^{n}$ are linearly dependent over 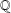 $\mathbb{Q}$, generate the same number field of degree at most two. This completes a result of Riffaut [‘Equations with powers of singular moduli’, Int. J. Number Theory, to appear], who proved the above theorem except for two explicit pairs of exceptions consisting of numbers of degree three. The purpose of this article is to treat these two remaining cases.
$\mathbb{Q}$, generate the same number field of degree at most two. This completes a result of Riffaut [‘Equations with powers of singular moduli’, Int. J. Number Theory, to appear], who proved the above theorem except for two explicit pairs of exceptions consisting of numbers of degree three. The purpose of this article is to treat these two remaining cases.
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
- 1
- Cited by


