Article contents
Laurent expansion of Dirichlet series
Published online by Cambridge University Press: 17 April 2009
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 〈an〉 be an increasing sequence of real numbers and 〈bn a sequence of positive real numbers. We deal here with the Dirichlet series 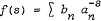 and its Laurent expansion at the abscissa of convergence, λ, say. When an and bn behave like
and its Laurent expansion at the abscissa of convergence, λ, say. When an and bn behave like
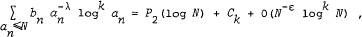
as N → ∞, where P2(x) is a certain polynomial, we obtain the Laurent expansion of f (s) at s = λ, namely
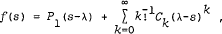
where P1(x) is a polynomial connected with P2(x) above. Also, the connection between P1 and P2 is made intuitively transparent in the proof.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1986
References
[1]Balakrishnan, U., ‘On the Laurent expansion of ζ(s, a) at s = 1’, J. Indian Math. Soc. 46 (1982), 181–187.Google Scholar
[2]Berndt, B.C., ‘On the Hurwitz zeta function’, Rocky mountain J. Math., 2 (1972), 151–157.CrossRefGoogle Scholar
[3]Briggs, W.E. and Buschman, R. G., ‘The power series coefficients of functions defined by Dirichlet series’, Illinois J. Math., 5 (1961), 43–44.CrossRefGoogle Scholar
[4]Knopfmacher, J., ‘Generalised Euler constants’, Proc. Edinburgh Math. Soc., 21 (1978), 25–32.CrossRefGoogle Scholar
- 3
- Cited by


