KRONECKER CLASSES, NORMAL COVERINGS AND CHIEF FACTORS OF GROUPS

Abstract

For a group G, a subgroup 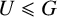$U \leqslant G$ and a group A such that 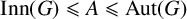$\mathrm {Inn}(G) \leqslant A \leqslant \mathrm {Aut}(G)$, we say that U is an A-covering group of G if 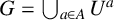$G = \bigcup _{a\in A}U^a$. A theorem of Jordan (1872), implies that if G is a finite group, 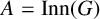$A = \mathrm {Inn}(G)$ and U is an A-covering group of G, then 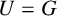$U = G$. Motivated by a question concerning Kronecker classes of field extensions, Neumann and Praeger (1990) conjectured that, more generally, there is an integer function f such that if G is a finite group and U is an A-covering subgroup of G, then 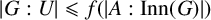$|G:U| \leqslant f(|A:\mathrm {Inn}(G)|)$. A key piece of evidence for this conjecture is a theorem of Praeger [‘Kronecker classes of fields and covering subgroups of finite groups’, J. Aust. Math. Soc. 57 (1994), 17–34], which asserts that there is a two-variable integer function g such that if G is a finite group and U is an A-covering subgroup of G, then 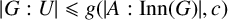$|G:U|\leqslant g(|A:\mathrm {Inn}(G)|,c)$, where c is the number of A-chief factors of G. Unfortunately, the proof of this theorem contains an error. In this paper, using a different argument, we give a correct proof of the theorem.