Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fitzgibbon, W.E.
1990.
Weakly continuous accretive operators in general Banach spaces.
Bulletin of the Australian Mathematical Society,
Vol. 41,
Issue. 2,
p.
185.
Bogachev, V. I.
1995.
Deterministic and stochastic differential equations in infinite-dimensional spaces.
Acta Applicandae Mathematicae,
Vol. 40,
Issue. 1,
p.
25.
Andres, Jan
and
Górniewicz, Lech
2003.
Topological Fixed Point Principles for Boundary Value Problems.
p.
233.


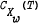 .
.