Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T06:20:07.105Z Has data issue: false hasContentIssue false
  • English
  • Français

JEŚMANOWICZ’ CONJECTURE ON PYTHAGOREAN TRIPLES

Part of: Diophantine equations

Published online by Cambridge University Press:  13 March 2017

MI-MI MA  and
YONG-GAO CHEN
MI-MI MA
Affiliation:
School of Mathematics and Statistics, Wuhan University, Wuhan 430072, PR China email [email protected]
YONG-GAO CHEN*
Affiliation:
School of Mathematical Sciences and Institute of Mathematics, Nanjing Normal University, Nanjing 210023, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1956, Jeśmanowicz conjectured that, for any positive integers 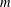$m$ and $n$ with 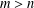$m>n$, 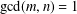$\gcd (m,n)=1$ and 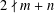$2\nmid m+n$, the Diophantine equation 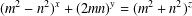$(m^{2}-n^{2})^{x}+(2mn)^{y}=(m^{2}+n^{2})^{z}$ has only the positive integer solution 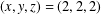$(x,y,z)=(2,2,2)$. In this paper, we prove the conjecture if 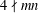$4\nmid mn$ and 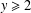$y\geq 2$.

Keywords

Jeśmanowicz’ conjectureDiophantine equationPythagorean triple

MSC classification

Primary: 11D61: Exponential equations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 1 , August 2017 , pp. 30 - 35
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the National Natural Science Foundation of China, grant no. 11371195, and a project funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions.

References

Deng, M. J. and Cohen, G. L., ‘On the conjecture of Jeśmanowicz concerning Pythagorean triples’, Bull. Aust. Math. Soc. 57 (1998), 515–524.Google Scholar
Jeśmanowicz, L., ‘Several remarks on Pythagorean numbers’, Wiad. Mat. 1 (1955/56), 196–202 (in Polish).Google Scholar
Le, M. H., ‘A note on Jeśmanowicz conjecture’, Colloq. Math. 69 (1995), 47–51.Google Scholar
Lu, W. T., ‘On the Pythagorean numbers 4n 2 - 1, 4n and 4n 2 + 1’, Acta Sci. Natur. Univ. Szechuan 2 (1959), 39–42 (in Chinese).Google Scholar
Miyazaki, T., ‘On the conjecture of Jeśmanowicz concerning Pythagorean triples’, Bull. Aust. Math. Soc. 80 (2009), 413–422.Google Scholar
Miyazaki, T., ‘Jeśmanowicz’ conjecture on exponential Diophantine equations’, Funct. Approx. Comment. Math. 45 (2011), 207–229.Google Scholar
Miyazaki, T., ‘Generalizations of classical results on Jeśmanowicz’ conjecture concerning Pythagorean triples’, J. Number Theory 133 (2013), 583–595.Google Scholar
Miyazaki, T. and Terai, N., ‘On Jeśmanowicz’ conjecture concerning Pythagorean triples II’, Acta Math. Hungar. 147 (2015), 286–293.Google Scholar
Miyazaki, T., Yuan, P. Z. and Wu, D. Y., ‘Generalizations of classical results on Jeśmanowicz’ conjecture concerning Pythagorean triples II’, J. Number Theory 141 (2014), 184–201.Google Scholar
Sierpiński, W., ‘On the Diophantine equation 3 x + 4 y = 5 z ’, Wiad. Mat. 1 (1955/56), 194–195 (in Polish).Google Scholar
Takakuwa, K., ‘On a conjecture on Pythagorean numbers, III’, Proc. Japan Acad. Ser. A Math. Sci. 69 (1993), 345–349.Google Scholar
Takakuwa, K., ‘A remark on Jeśmanowicz’ conjecture’, Proc. Japan Acad. Ser. A Math. Sci. 72 (1996), 109–110.Google Scholar
Takakuwa, K. and Asaeda, Y., ‘On a conjecture on Pythagorean numbers, II’, Proc. Japan Acad. Ser. A Math. Sci. 69 (1993), 287–290.Google Scholar
Tang, M. and Weng, J. X., ‘Jeśmanowicz’ conjecture with Fermat numbers’, Taiwanese J. Math. 18 (2014), 925–930.Google Scholar
Terai, N., ‘On Jeśmanowicz’ conjecture concerning primitive Pythagorean triples’, J. Number Theory 141 (2014), 316–323.Google Scholar