Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-12T03:59:59.068Z Has data issue: false hasContentIssue false
  • English
  • Français

Isotropic varieties in the singular symplectic geometry

Published online by Cambridge University Press:  17 April 2009

Stanisław Janeczko  and
Adam Kowalczyk
Stanisław Janeczko
Affiliation:
Department of Mathematics, Monash University, Clayton, Vic. 3168, Australia Institute of Math, Technical University of Warsaw, Pl. Jednosci Robotniczej 1, 00661 Warsaw, Poland
Adam Kowalczyk
Affiliation:
Telecom Australia, Research Laboratories, 770 Blacburn Rd., Clayton, Vic. 3168
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Maximal isotropic varieties of the singular symplectic structure 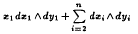on R2n are characterised in terms of generating families. The normal forms of the simplest singularities (of codimension 1) are obtained with the help of the theory of boundary singularities.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 38 , Issue 2 , October 1988 , pp. 161 - 169
Copyright
Copyright © Australian Mathematical Society 1988

References

[1]Abraham, R. and Marsden, J.E., Foundations of Mechanics (Benjamin/Cummings, Reading, 1978).Google Scholar
[2]Arnold, V.I., Gusein-Zade, S.M., and Varchenko, A.N., Singularities of Differentiable Maps 1, Engl. ed. (Birkhauser, Boston, 1985).CrossRefGoogle Scholar
[3]Arnold, V.I., ‘Singularities of systems of rays’, Russian Math. Surveys 38 (1983), 87–176.CrossRefGoogle Scholar
[4]Bröcker, Th. and Lander, L., Differentiable Germs and Catastrophes (Cambridge University Press, Cambridge, 1975).CrossRefGoogle Scholar
[5]Duistermaat, J.J., ‘Oscilatory integrals, lagrange immersions and unfoldings of singularities’, Comm. Pure Appl. Math. 27 (1974), 207–281.CrossRefGoogle Scholar
[6]Janeczko, S., ‘Constrained Lagrangian submanifolds over singular constraining varieties and discriminant varieties’, Ann. Inst. H. Poincaré, Sect A. (N.S.) 40 (1987), 1–25.Google Scholar
[7]Janeczko, S., ‘Generating families for images of lagrangian submanifolds and open swallowtails’, Math. Proc. Cambridge Phił. Soc. 10 (1986), 91–107.CrossRefGoogle Scholar
[8]Janeczko, S., ‘Geometrical approach to phase transitions and singularities of Lagrangian submanifolds’, Demonstratio Math. 16 (1983), 487–502.Google Scholar
[9]Janeczko, S., ‘On singular lagrangian submanifolds and thermodynamics’, Ann. Soc. Sci. Bruxelles Ser. I. 99 (1985), 49–83.Google Scholar
[10]Martinet, J., Singularities of Smooth Functions and Maps (Cambridge Univ. Press, Cambridge, 1982).Google Scholar
[11]Martinet, J., ‘Sur les singularites des formnes differentielles’, Ann. Inst. Fourier (Grenoble) 20 (1970), 95–178.CrossRefGoogle Scholar
[12]Poston, T. and Stewart, I., Catastrophe Theory and its Applications (Pitman, San Francisco, 1978).Google Scholar
[13]Thom, R., Structural Stability and Morphogenesis (Benjamin, New York, 1975).Google Scholar
[14]Wall, C.T.C., ‘Geometric properties of generic differentiable manifolds’, in Geometry and Topology: Lecture Notes in Math 597, Dold, A. and Eckmann, B., editors, pp. 707–774 (Springer-Verlag, 1977).CrossRefGoogle Scholar
[15]Weinstein, A., Lectures on Symplectic Manifolds (CBMS Regional Conf. Ser. in Math., 1977).CrossRefGoogle Scholar
[16]Zakalyukin, V.M., ‘Lagrangian and Legrendrian singularities’, Functional Anal. Appl. 10 (1976), 23–31.CrossRefGoogle Scholar