Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pini, R.
and
Singh, C.
1997.
A survey of recent[1985-1995]advances in generalized convexity with applications to duality theory and optimality conditions.
Optimization,
Vol. 39,
Issue. 4,
p.
311.


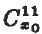 -class (that is, each
-class (that is, each 