Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-17T13:02:59.112Z Has data issue: false hasContentIssue false
  • English
  • Français

Interior regularity of the degenerate Monge-Ampère equation

Published online by Cambridge University Press:  17 April 2009

Zbigniew Błocki
Zbigniew Błocki
Affiliation:
Jagiellonian University, Institute of Mathematics, Reymonta 4, 30-059 Kraków, Poland e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study interior C1,1 regularity of generalised solutions of the Monge-Ampére equation det D2u = ψ, ψ ≥ 0, on a bounded convex domain Ω in ℝn with u = ϕ on ∂Ω. We prove in particular that u ∈ C1,1(Ω) if either i) ϕ = 0 and ψ1/(n − 1) ∈ C1,1 (Ω) or ii) Ω is C1,1 strongly convex, ϕ ∈ C1,1 (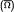), ψ1/(n − 1) ∈ C1,1(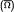) and ψ > 0 on U ∩ Ω, where U is a neighbourhood of ∂Ω. The main tool is an improvement of Pogorelov's well known C1,1 estimate so that it can be applied to the degenerate case.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 68 , Issue 1 , August 2003 , pp. 81 - 92
Copyright
Copyright © Australian Mathematical Society 2003

References

[1]Aleksandrov, A.D., ‘Smoothness of a convex surface of bounded Gaussian curvature’, Dokl. Akad. Nauk SSSR 36 (1942), 195–199.Google Scholar
[2]Blocki, Z., ‘Smooth exhaustion functions in convex domains’, Proc. Amer. Math. Soc. 125 (1997), 477–484.CrossRefGoogle Scholar
[3]Blocki, Z., ‘Interior regularity of the complex Monge-Ampère equation in convex domains’, Duke Math. J. 105 (2000), 167–181.CrossRefGoogle Scholar
[4]Blocki, Z., ‘The C 1,1 regularity of the pluricomplex Green function’, Michigan Math. J. 47 (2000), 211–215.CrossRefGoogle Scholar
[5]Blocki, Z., ‘Regularity of the pluricomplex Green function with several poles’, Indiana Univ Math. J. 50 (2001), 335–351.CrossRefGoogle Scholar
[6]Caffarelli, L., Nirenberg, L. and Spruck, J., ‘The Dirichlet problem for nonlinear second order elliptic equations I: Monge-Ampère equation’, Comm. Pure Appl. Math. 37 (1984), 369–402.CrossRefGoogle Scholar
[7]Cheng, S.-Y. and Yau, S.-T., ‘Differential equations on Riemannian manifolds and their geometric applications’, Comm. Pure Appl. Math. 28 (1975), 333–354.CrossRefGoogle Scholar
[8]Cheng, S.-Y. and Yau, S.-T., ‘On the regularity of the Monge-Ampère equation det (∂2u/∂x i∂x j)= F(x, u)’, Comm. Pure Appl. Math. 30 (1977), 41–68.CrossRefGoogle Scholar
[9]Cheng, S.-Y. and Yau, S.-T., ‘The real Monge-Ampère equation and affine flat structures’, in Proc. Symp. Diff. Geom. Diff. Eq. (Beijing, 1980) 1, (Chern, S.S. and Wu, W.T., Editors) (Science Press, Beijing, 1982), pp. 339–370.Google Scholar
[10]Cheng, S.-Y. and Yau, S.-T., ‘On the existence of a complete Kähler metric on non-compact complex manifolds and the regularity of Fefferman's equation’, Comm. Pure Appl. Math. 33 (1980), 507–544.CrossRefGoogle Scholar
[11]Guan, B., ‘The Dirichlet problem for complex Monge-Ampère equations and regularity of the pluri-complex Green function’, Comm. Anal. Geom. 6 (1998), 687–703; Correction: Comm. Anal. Geom. 8 (2000), 213–218.CrossRefGoogle Scholar
[12]Guan, P., ‘C 2 priori estimates for degenerate Monge-Ampere equations’, Duke Math. J. 86 (1997), 323–346.CrossRefGoogle Scholar
[13]Guan, P., Trudinger, N.S. and Wang, X.-J., ‘On the Dirichlet problem for degenerate Mong-Ampère equations’, Acta Math. 182 (1999), 87–104.CrossRefGoogle Scholar
[14]Ivochkina, N.M., ‘Construction of a priori bounds for convex solutions of the Monge-Ampere equation by integral methods’, Ukrainian Math. J. 30 (1978), 32–38.CrossRefGoogle Scholar
[15]Krylov, N.V., ‘Boundedly inhomogeneous elliptic and parabolic equations in a domain’, (in Russian), Izv. Acad. Nauk SSSR Ser. Mat. 47 (1983), 75–108; English translation: Math. USSR-Izv. 22 (1984), 67–98.Google Scholar
[16]Pogorelov, A. V., ‘Soviet Math. Dokl.’, Dokl. Akad. Nauk SSSR 12 (1971), 1436–1440.Google Scholar
[17]Rauch, J. and Taylor, B.A., ‘The Dirichlet problem for the multidimensional Monge-Ampère equation’, Rocky Mountain Math. J. 7 (1977), 345–364.CrossRefGoogle Scholar
[18]Schulz, F., ‘A C 2 -estimate for solutions of complex Monge-Ampère equations’, J. Reine Angew. Math. 348 (1984), 88–93.Google Scholar
[19]Trudinger, N.S. and Urbas, J., ‘On second derivative eatimates for equations of Monge-Ampère type’, Bull. Austral. Math. Soc. 28 (1983), 321–334.Google Scholar
[20]Urbas, J., ‘Regularity of generalized solutions of the Monge-Ampère equation’, Math Z. 197 (1988), 365–393.CrossRefGoogle Scholar
[21]Wang, X.-J., ‘Some counterexamples to the regularity of Monge-Ampère equations’ Proc. Amer. Math. Soc. 123 (1995), 841–845.Google Scholar