Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T21:05:25.306Z Has data issue: false hasContentIssue false
  • English
  • Français

INTEGRAL MEANS OF HOLOMORPHIC FUNCTIONS AS GENERIC LOG-CONVEX WEIGHTS

Part of: Spaces and algebras of analytic functions Holomorphic functions of several complex variables

Published online by Cambridge University Press:  07 August 2017

EVGUENI DOUBTSOV Open the ORCID record for EVGUENI DOUBTSOV [Opens in a new window]
EVGUENI DOUBTSOV*
Affiliation:
St. Petersburg Department of V.A. Steklov Mathematical Institute, Fontanka 27, St. Petersburg 191023, Russia Department of Mathematics and Mechanics, St. Petersburg State University, Universitetski pr. 28, St. Petersburg 198504, Russia email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 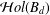${\mathcal{H}}ol(B_{d})$ denote the space of holomorphic functions on the unit ball 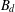$B_{d}$ of 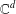$\mathbb{C}^{d}$, 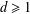$d\geq 1$. Given a log-convex strictly positive weight 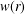$w(r)$ on 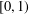$[0,1)$, we construct a function 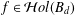$f\in {\mathcal{H}}ol(B_{d})$ such that the standard integral means 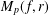$M_{p}(f,r)$ and 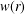$w(r)$ are equivalent for any 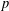$p$ with 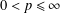$0<p\leq \infty$. We also obtain similar results related to volume integral means.

Keywords

Hardy convexity theoremvolume integral meanslog-convex weight

MSC classification

Primary: 32A10: Holomorphic functions
Secondary: 30H10: Hardy spaces 32A35: $H^p$-spaces, Nevanlinna spaces 32A36: Bergman spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 1 , February 2018 , pp. 88 - 93
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Abakumov, E. and Doubtsov, E., ‘Moduli of holomorphic functions and logarithmically convex radial weights’, Bull. Lond. Math. Soc. 47(3) (2015), 519–532.Google Scholar
Hardy, G. H., ‘The mean value of the modulus of an analytic function’, Proc. Lond. Math. Soc. 14 (1914), 269–277.Google Scholar
Ryll, J. and Wojtaszczyk, P., ‘On homogeneous polynomials on a complex ball’, Trans. Amer. Math. Soc. 276(1) (1983), 107–116.Google Scholar
Taylor, A. E., ‘New proofs of some theorems of Hardy by Banach space methods’, Math. Mag. 23 (1950), 115–124.CrossRefGoogle Scholar
Wang, C., Xiao, J. and Zhu, K., ‘Logarithmic convexity of area integral means for analytic functions II’, J. Aust. Math. Soc. 98(1) (2015), 117–128.Google Scholar
Wang, C. and Zhu, K., ‘Logarithmic convexity of area integral means for analytic functions’, Math. Scand. 114(1) (2014), 149–160.Google Scholar
Xiao, J. and Zhu, K., ‘Volume integral means of holomorphic functions’, Proc. Amer. Math. Soc. 139(4) (2011), 1455–1465.Google Scholar