Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-20T07:27:57.694Z Has data issue: false hasContentIssue false
  • English
  • Français

INJECTIVE LINEAR TRANSFORMATIONS WITH EQUAL GAP AND DEFECT

Part of: Semigroups Basic linear algebra

Published online by Cambridge University Press:  18 May 2021

C. MENDES ARAÚJO Open the ORCID record for C. MENDES ARAÚJO [Opens in a new window]  and
S. MENDES-GONÇALVES Open the ORCID record for S. MENDES-GONÇALVES [Opens in a new window]
C. MENDES ARAÚJO
Affiliation:
CMAT–Centro de Matemática, Universidade do Minho, Campus de Gualtar, 4710-057 Braga, Portugal e-mail: [email protected]
S. MENDES-GONÇALVES*
Affiliation:
CMAT–Centro de Matemática, Universidade do Minho, Campus de Gualtar, 4710-057 Braga, Portugal
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

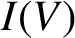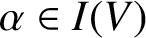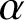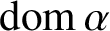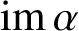Let V be an infinite-dimensional vector space over a field F and let $I(V)$ be the inverse semigroup of all injective partial linear transformations on V. Given $\alpha \in I(V)$ , we denote the domain and the range of $\alpha $ by ${\mathop {\textrm {dom}}}\,\alpha $ and ${\mathop {\textrm {im}}}\,\alpha $ , and we call the cardinals 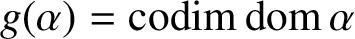$g(\alpha )={\mathop {\textrm {codim}}}\,{\mathop {\textrm {dom}}}\,\alpha $ and 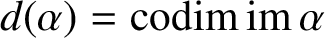$d(\alpha )={\mathop {\textrm {codim}}}\,{\mathop {\textrm {im}}}\,\alpha $ the ‘gap’ and the ‘defect’ of 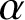$\alpha $ . We study the semigroup 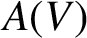$A(V)$ of all injective partial linear transformations with equal gap and defect and characterise Green’s relations and ideals in 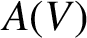$A(V)$ . This is analogous to work by Sanwong and Sullivan [‘Injective transformations with equal gap and defect’, Bull. Aust. Math. Soc. 79 (2009), 327–336] on a similarly defined semigroup for the set case, but we show that these semigroups are never isomorphic.

Keywords

idealsinjective linear transformationsGreen’s relationsquasiresiduals

MSC classification

Primary: 20M20: Semigroups of transformations, etc.
Secondary: 15A04: Linear transformations, semilinear transformations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 106 - 116
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the authors was partially financed by Portuguese Funds through FCT (Fundação para a Ciência e a Tecnologia) within the Projects UIDB/00013/2020 and UIDP/00013/2020.

References

Clifford, A. H. and Preston, G. B., The Algebraic Theory of Semigroups, Vols 1 and 2, Mathematical Surveys, 7 (American Mathematical Society, Providence, RI, 1961 and 1967).Google Scholar
Howie, J. M., Fundamentals of Semigroup Theory, London Mathematical Society Monographs (NS), 12 (Clarendon Press, Oxford, 1995).Google Scholar
Mendes-Gonçalves, S. and Sullivan, R. P., ‘Maximal inverse subsemigroups of the symmetric inverse semigroup on a finite-dimensional vector space’, Comm. Algebra 34(3) (2006), 1055–1069.CrossRefGoogle Scholar
Mitsch, H., ‘A natural partial order for semigroups’, Proc. Amer. Math. Soc. 97(3) (1986), 384–388.CrossRefGoogle Scholar
Mitsch, H., ‘A property of transformation semigroups’, Semigroup Forum 85(1) (2012), 91–96.CrossRefGoogle Scholar
Mitsch, H., ‘Quasiresiduals in semigroups with natural partial order’, Algebra Colloq. 24(3) (2017), 361–380.CrossRefGoogle Scholar
Sanwong, J. and Sullivan, R. P., ‘Injective transformations with equal gap and defect’, Bull. Aust. Math. Soc. 79 (2009), 327–336.CrossRefGoogle Scholar