Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T00:59:15.932Z Has data issue: false hasContentIssue false
  • English
  • Français

INFINITE FAMILIES OF CONGRUENCES FOR OVERPARTITIONS WITH RESTRICTED ODD DIFFERENCES

Part of: Additive number theory; partitions Combinatorics

Published online by Cambridge University Press:  08 January 2020

BERNARD L. S. LIN Open the ORCID record for BERNARD L. S. LIN [Opens in a new window] ,
JIAN LIU Open the ORCID record for JIAN LIU [Opens in a new window] ,
ANDREW Y. Z. WANG Open the ORCID record for ANDREW Y. Z. WANG [Opens in a new window]  and
JIEJUAN XIAO Open the ORCID record for JIEJUAN XIAO [Opens in a new window]
BERNARD L. S. LIN
Affiliation:
School of Science, Jimei University, Xiamen361021, P. R. China email [email protected]
JIAN LIU
Affiliation:
School of Insurance, Central University of Finance and Economics, Beijing102206, P. R. China email [email protected]
ANDREW Y. Z. WANG*
Affiliation:
School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu611731, P. R. China email [email protected]
JIEJUAN XIAO
Affiliation:
School of Science, Jimei University, Xiamen361021, P. R. China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 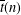$\overline{t}(n)$ be the number of overpartitions in which (i) the difference between successive parts may be odd only if the larger part is overlined and (ii) if the smallest part is odd then it is overlined. Ramanujan-type congruences for 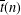$\overline{t}(n)$ modulo small powers of $2$ and 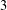$3$ have been established. We present two infinite families of congruences modulo 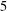$5$ and 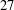$27$ for 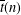$\overline{t}(n)$, the first of which generalises a recent result of Chern and Hao [‘Congruences for two restricted overpartitions’, Proc. Math. Sci. 129 (2019), Article 31].

Keywords

overpartitioncongruencedissection

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 1 , August 2020 , pp. 59 - 66
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the National Natural Science Foundation of China (No. 11871246), the Natural Science Foundation of Fujian Province of China (No. 2019J01328) and the Program for New Century Excellent Talents in Fujian Province University (No. B17160).

References

Alaca, A., Alaca, S., Lemire, M. F. and Williams, K. S., ‘Nineteen quaternary quadratic forms’, Acta Arith. 130 (2007), 277–310.CrossRefGoogle Scholar
Berndt, B. C., Ramanujan’s Notebooks, Part III (Springer, New York, 1991).CrossRefGoogle Scholar
Berndt, B. C., Number Theory in the Spirit of Ramanujan (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
Bringmann, K., Dousse, J., Lovejoy, J. and Mahlburg, K., ‘Overpartitions with restricted odd differences’, Electron. J. Combin. 22 (2015), Article ID P3.17.CrossRefGoogle Scholar
Chen, W. Y. C. and Xia, E. X. W., ‘Proof of a conjecture of Hirschhorn and Sellers on overpartitions’, Acta Arith. 163 (2014), 59–69.10.4064/aa163-1-5CrossRefGoogle Scholar
Chern, S. and Hao, L.-J., ‘Congruences for two restricted overpartitions’, Proc. Math. Sci. 129 (2019), Article 31.CrossRefGoogle Scholar
Hirschhorn, M. D., The Power of q. A Personal Journey (Springer, Cham, 2017).CrossRefGoogle Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic relations for overpartitions’, J. Combin. Math. Combin. Comput. 53 (2005), 65–73.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Congruences for overpartitions with restricted odd differences’, Ramanujan J., to appear, https://doi.org/10.1007/s11139-019-00156-x.CrossRefGoogle Scholar
Lin, B. L. S., ‘A new proof of a conjecture of Hirschhorn and Sellers on overpartitions’, Ramanujan J. 38 (2015), 199–209.CrossRefGoogle Scholar
Lovejoy, J. and Osburn, R., ‘Quadratic forms and four partition functions modulo 3’, Integers 11 (2011), Article 4.10.1515/integ.2011.004CrossRefGoogle Scholar
Naika, M. S. M. and Gireesh, D. S., ‘Congruences for overpartitions with restricted odd differences’, Afrika Mat. 30 (2019), 1–21.CrossRefGoogle Scholar
Xia, E. X. W. and Yao, O. X. M., ‘New Ramanujan-like congruences modulo powers of 2 and 3 for overpartitions’, J. Number Theory 133 (2013), 1932–1949.Google Scholar
Zhao, H. and Zhong, Z., ‘Ramanujan type congruences for a partition function’, Electron. J. Combin. 18 (2011), Article ID P58.CrossRefGoogle Scholar